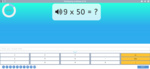
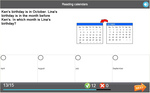
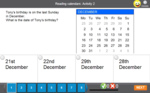
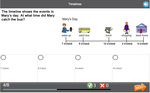
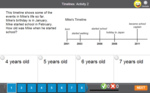
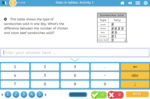
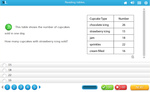
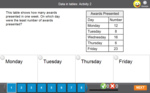
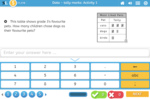
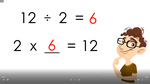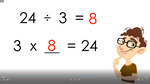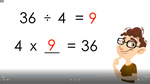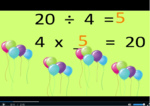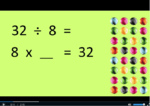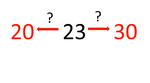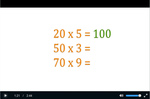Mathematics – United States – Common Core State Standards
3.OA – Operations & Algebraic Thinking
Mathematics
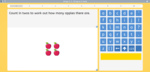
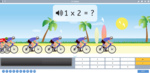
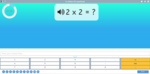
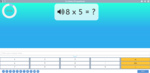
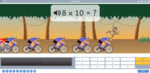
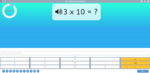
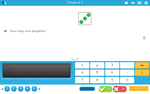
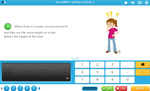
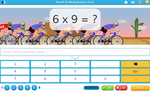
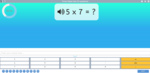
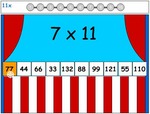
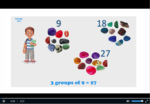
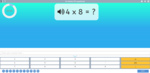
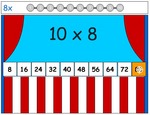
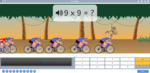
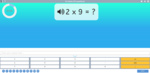
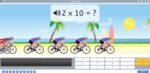
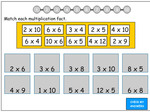
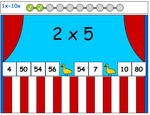
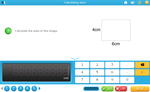
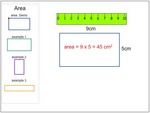
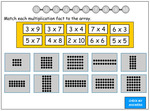
3.OA.1 – Interpret products of whole numbers, e.g., interpret 5 × 7 as the total number of objects in 5 groups of 7 objects each. For example, describe a context in which a total number of objects can be expressed as 5 × 7.
-
18 learning outcomes – click to view
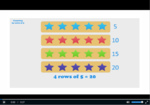
Samples: Groups of 2. Groups of 5. Groups of 10. Counting on number line (by 2's). Counting on number line (by 5's).
-
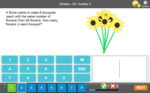
Groups of two
- Activities: 4 course, 7 extra
-
-
- Groups of 2
- Tutorial
-
-
-
- Counting in two's - rows
- Practice
-
-
-
- Counting in two's - groups
- Practice
-
-
-
- Groups of 2
- Tutorial
-
Extra activities
-
-
- Groups of 2
- Printable
-
-
-
- Groups of 2
- Printable
-
-
-

- Groups of 2
- Practice
-
-
-

- Groups of 2
- Challenge
-
-
-

- Groups of 2
- Assessment
-
-
-

- Multiply by adding lots of 2
- Practice
-
-
Groups of five
- Activities: 5 course, 14 extra
-
-
- Groups of 5
- Tutorial
-
-
-
- Rows of 5
- Practice
-
-
-
- Groups of 5
- Practice
-
-
-
- Groups of 5
- Tutorial
-
-
-
- Rows of 5
- Tutorial
-
Extra activities
-
-
- Groups of 5
- Printable
-
-
-
- Groups of 5
- Printable
-
-
-
- Groups of 5
- Printable
-
-
-
- Identifying the amounts in a group
- Tutorial
-
-
-
- Groups and rows of 5
- Tutorial
-
-
-
- Groups of 5
- Tutorial
-
-
-
- Rows of 5
- Tutorial
-
-
-

- Groups of 5
- Challenge
-
-
-

- Groups of 5
- Practice
-
-
-

- Multiply by adding lots of 5
- Practice
-
-
-

- Groups of 5
- Assessment
-
-
-

- Rows of five
- Practice
-
-
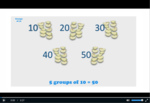
Groups of ten
- Activities: 6 course, 5 extra
-
-
- Groups of 10
- Tutorial
-
-
-
- Number of tens
- Practice
-
-
-
- Rows of 10
- Practice
-
-
-
- Groups of 10
- Practice
-
-
-
- Groups of 10
- Tutorial
-
-
-
- Rows Of 10
- Tutorial
-
Extra activities
-
-
- Groups of 10
- Printable
-
-
-
- Groups of 10
- Printable
-
-
-

- Groups of 10
- Challenge
-
-
-

- Rows of ten
- Practice
-
-
-

- Groups of 10
- Assessment
-
-
Counting on by two on a number line
- Activities: 7 course, 5 extra
-
-
- Counting on number line (by 2's)
- Tutorial
-
-
-
- Counting by 2
- Practice
-
-
-
- Counting by 2
- Practice
-
-
-
- Counting by 2
- Practice
-
-
-
- Counting by 2
- Tutorial
-
-
-
- Counting by 2
- Tutorial
-
-
-
- Counting by Two - Faster
- Tutorial
-
Extra activities
-
-
- Counting by 2
- Printable
-
-
-
- Counting by 2
- Tutorial
-
-
-

- Counting by 2
- Assessment
-
-
-

- Count on by 2 the next three numbers
- Practice
-
-
-

- Count by lots of 2
- Practice
-
-
Counting on by five on a number line
- Activities: 6 course, 3 extra
-
-
- Counting on number line (by 5's)
- Tutorial
-
-
-
- Counting by 5
- Tutorial
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Tutorial
-
Extra activities
-
-
- Counting by 5
- Printable
-
-
-

- Counting by 5
- Assessment
-
-
-

- Count by lots of 5
- Practice
-
-
Counting on by ten on a number line
- Activities: 6 course, 5 extra
-
-
- Counting on number line (by 10's)
- Tutorial
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Tutorial
-
-
-
- Counting by 10
- Tutorial
-
Extra activities
-
-
- Counting by 10
- Printable
-
-
-
- Counting by 10
- Printable
-
-
-

- Numbers Problem Solving
- Assessment
-
-
-

- Count by lots of 10
- Practice
-
-
-

- Counting by 10
- Assessment
-
-
Arrays
- Activities: 4 course, 0 extra
-
-
- Arrays 2, 5, 10 (up to 5 rows)
- Practice
-
-
-
- Arrays 2, 5, 10 (up to 10 rows)
- Practice
-
-
-
- Arrays
- Practice
-
-
-
- Arrays 2, 5, 10 (up to 5 rows)
- Practice
-
-
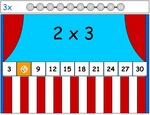
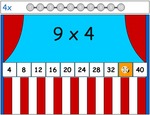
2x tables
- Activities: 12 course, 6 extra
-
-
- Groups of 2
- Tutorial
-
-
-
- Learning 2x tables
- Tutorial
-
-
-
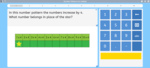
- Number Patterns (2x tables)
- Practice
-
-
-
- 2x tables - matching answers
- Practice
-
-
-
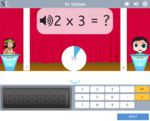
- 2x tables
- Practice
-
-
-
- 2x tables (20 questions)
- Practice
-
-
-
- 2x tables
- Challenge
-
-
-
- 2x tables
- Tutorial
-
-
-
- Time tables match (2x)
- Practice
-
-
-
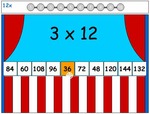
- 3x tables learn
- Practice
-
-
-
- 2x Tables
- Practice
-
-
-
- Test 2 X
- Practice
-
Extra activities
-
-
- 2x tables
- Printable
-
-
-
- Times Tables Chart
- Printable
-
-
-

- 2X tables
- Practice
-
-
-

- 2X tables
- Assessment
-
-
-

- Drill - 2X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 2X tables
- Printable
-
-
5x tables
- Activities: 9 course, 7 extra
-
-
- Groups of 5
- Tutorial
-
-
-
- Learning 5x tables
- Tutorial
-
-
-
- Number Patterns (5x tables)
- Practice
-
-
-
- 5x tables
- Practice
-
-
-
- 5x tables
- Practice
-
-
-
- 5x tables (20 questions)
- Practice
-
-
-
- 5x tables
- Challenge
-
-
-
- 5x tables
- Tutorial
-
-
-
- Counting by 5's on a clock face
- Tutorial
-
Extra activities
-
-
- 5x tables
- Printable
-
-
-
- 5x tables
- Printable
-
-
-
- 5x tables
- Printable
-
-
-

- 5X tables
- Practice
-
-
-

- Drill - 5X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 5X tables
- Printable
-
-
-

- 5X tables
- Assessment
-
-
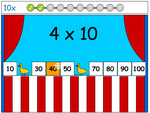
10x tables
- Activities: 9 course, 6 extra
-
-
- Groups of 10
- Tutorial
-
-
-
- Learning 10x tables
- Tutorial
-
-
-
- Number Patterns (10x tables)
- Practice
-
-
-
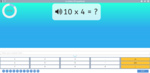
- 10x tables
- Practice
-
-
-
- 10x tables
- Practice
-
-
-
- 10x tables (20 questions)
- Practice
-
-
-
- 10x tables
- Challenge
-
-
-
- 10x tables
- Printable
-
-
-
- 10x tables
- Tutorial
-
Extra activities
-
-
- 10x tables
- Printable
-
-
-
- 10x tables
- Printable
-
-
-

- 10 X Tables
- Practice
-
-
-

- Drill - 10X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 10X tables
- Printable
-
-
-

- 10X tables
- Assessment
-
-
2x tables (problem solving)
- Activities: 2 course, 7 extra
-
-
- 2x tables (problem solving)
- Practice
-
-
-
- 2x tables (problem solving)
- Practice
-
Extra activities
-
-
- 2x tables (problem solving)
- Printable
-
-
-
- 2x tables (problem solving)
- Printable
-
-
-
- 2x tables (problem solving)
- Printable
-
-
-
- 2x tables (problem solving)
- Printable
-
-
-
- 2x tables (problem solving)
- Printable
-
-
-
- 2x tables (problem solving) answer sheet
- Printable
-
-
-
- 2x tables (problem solving)
- Printable
-
-
5x tables (problem solving)
- Activities: 2 course, 6 extra
-
-
- 5x tables (problem solving)
- Practice
-
-
-
- 5x tables (problem solving)
- Practice
-
Extra activities
-
-
- 5x tables (problem solving)
- Printable
-
-
-
- 5x tables (problem solving)
- Printable
-
-
-
- 5x tables (problem solving)
- Printable
-
-
-
- 5x tables (problem solving)
- Printable
-
-
-
- 5x tables (problem solving)
- Printable
-
-
-
- 5x tables (problem solving) answer sheet
- Printable
-
-
10x tables (problem solving)
- Activities: 2 course, 6 extra
-
-
- 10x tables (problem solving)
- Practice
-
-
-
- 10x tables (problem solving)
- Practice
-
Extra activities
-
-
- 10x tables (problem solving)
- Printable
-
-
-
- 10x tables (problem solving)
- Printable
-
-
-
- 10x tables (problem solving)
- Printable
-
-
-
- 10x tables (problem solving)
- Printable
-
-
-
- 10x tables (problem solving)
- Printable
-
-
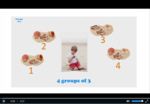
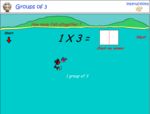
Number patterns and groups (of 3)
- Activities: 3 course, 1 extra
-
-
- Groups of 3
- Tutorial
-
-
-
- Rows of 3
- Tutorial
-
-
-
- Groups of 3
- Practice
-
Extra activities
-
-

- Groups of three
- Practice
-
-
3x tables (problem solving)
- Activities: 3 course, 3 extra
-
-
- 3x tables (problem solving)
- Practice
-
-
-
- 3x tables (problem solving)
- Practice
-
-
-
- 3x tables (problem solving)
- Practice
-
Extra activities
-
-
- 3x tables (problem solving)
- Printable
-
-
-
- 3x tables (problem solving)
- Printable
-
-
-
- 3x tables (problem solving)
- Printable
-
-
Groups and rows of 4
- Activities: 3 course, 4 extra
-
-
- Groups of 4
- Tutorial
-
-
-
- Rows of 4
- Tutorial
-
-
-
- Groups of 4
- Practice
-
Extra activities
-
-
- Groups of 4
- Tutorial
-
-
-
- Groups of four
- Printable
-
-
-
- Groups of four Answer sheet
- Printable
-
-
-

- Groups of four
- Practice
-
-
4x tables (problem solving)
- Activities: 3 course, 6 extra
-
-
- 4x tables (problem solving)
- Practice
-
-
-
- 4x tables (problem solving)
- Practice
-
-
-
- 4x tables (problem solving)
- Practice
-
Extra activities
-
-
- 4x tables (problem solving)
- Printable
-
-
-
- 4x tables (problem solving)
- Printable
-
-
-
- 4x tables (problem solving)
- Printable
-
-
-
- 4x tables (problem solving)
- Printable
-
-
-
- 4x tables (problem solving)
- Printable
-
-
-
- 4x tables (problem solving) answer sheet
- Printable
-
-
2x-10x tables
- Activities: 5 course, 7 extra
-
-
- Tricky 20
- Practice
-
-
-
- 2x-10x tables
- Practice
-
-
-
- 2x-10x tables
- Challenge
-
-
-
- Times Tables Test (25 questions)
- Practice
-
-
-
- Matching facts - Concentration Game
- Practice
-
Extra activities
-
-
- 2x-12x tables
- Printable
-
-
-
- 5X - 12X tables
- Printable
-
-
-
- 5X - 12X tables
- Printable
-
-
-
- 5X - 12X tables
- Printable
-
-
-

- Times Tables 11x
- Practice
-
-
-

- 5X - 12X tables
- Assessment
-
-
-

- Times Tables 12x
- Practice
-
-
-
18 learning outcomes – click to view
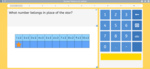
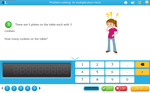
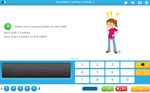
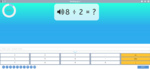
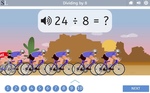
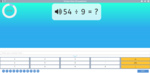
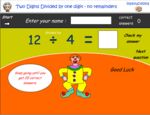
3.OA.2 – Interpret whole-number quotients of whole numbers, e.g., interpret 56 ÷ 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each. For example, describe a context in which a number of shares or a number of groups can be expressed as 56 ÷ 8.
-
8 learning outcomes – click to view
Samples: Sharing equally. Dividing by 2. Dividing by 2 (problem solving). Using the division symbol. Dividing by 3.
-
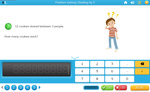
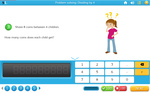
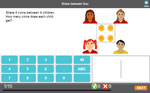
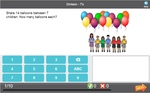
Sharing between 2
- Activities: 0 course, 5 extra
Extra activities
-
-

- Sharing equally
- Practice
-
-
-

- Share 12 equally
- Practice
-
-
-

- Share 16 equally
- Practice
-
-
-

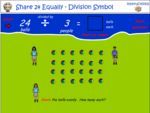
- Share 24 equally
- Practice
-
-
-

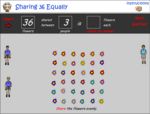
- Share 36 equally
- Practice
-
-
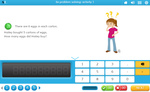
Dividing by 2
- Activities: 4 course, 1 extra
-
-
- Dividing by 2
- Tutorial
-
-
-
- Dividing by 2
- Practice
-
-
-
- Dividing by 2
- Practice
-
-
-
- Dividing by 2
- Tutorial
-
Extra activities
-
-
- Dividing by 2
- Printable
-
-
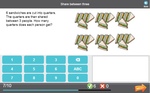
Dividing by 2 (problem solving)
- Activities: 2 course, 3 extra
-
-
- Dividing by 2 (problem solving)
- Practice
-
-
-
- Share between two - 2
- Practice
-
Extra activities
-
-
- Dividing by 2 (problem solving)
- Printable
-
-
-
- Dividing by 2 (problem solving)
- Printable
-
-
-
- Dividing by 2 (problem solving)
- Printable
-
-
Using the division symbol
- Activities: 3 course, 0 extra
-
-
- Using the division symbol
- Tutorial
-
-
-
- Using the division symbol
- Practice
-
-
-
- Dividing using division symbol
- Tutorial
-
-
Dividing by 3
- Activities: 4 course, 3 extra
-
-
- Dividing by 3
- Tutorial
-
-
-
- Dividing by 3
- Practice
-
-
-
- Share counters between three
- Practice
-
-
-
- Dividing by 3
- Tutorial
-
Extra activities
-
-
- Dividing by 3
- Printable
-
-
-
- Share counters between three
- Printable
-
-
Dividing by 3 (problem solving)
- Activities: 2 course, 2 extra
-
-
- Dividing by 3 (problem solving)
- Practice
-
-
-
- Dividing by 3
- Practice
-
Extra activities
-
-
- Dividing by 3 (problem solving)
- Printable
-
-
-
- Dividing by 3 (problem solving)
- Printable
-
-
Dividing by 4
- Activities: 4 course, 3 extra
-
-
- Dividing by 4
- Tutorial
-
-
-
- Dividing by 4
- Practice
-
-
-
- Dividing by 4
- Tutorial
-
-
-
- Share objects between four
- Printable
-
Extra activities
-
-
- Dividing by 4
- Printable
-
-
-
- Share objects between four
- Printable
-
-
-
- Share objects between four Answer sheet
- Printable
-
-
Dividing by 4 (problem solving)
- Activities: 2 course, 5 extra
-
-
- Dividing by 4 (problem solving)
- Practice
-
-
-
- Dividing by 4
- Practice
-
Extra activities
-
-
- Dividing by 4 (problem solving)
- Printable
-
-
-
- Dividing by 4 (problem solving)
- Printable
-
-
-
- Dividing by 4 (problem solving)
- Printable
-
-
-
- Dividing by 4 (problem solving)
- Printable
-
-
-
- Dividing by 4 - Answer sheet
- Printable
-
-
-
8 learning outcomes – click to view
3.OA.3 – Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem. (See Glossary, Table 2. http://www.corestandards.org/the-standards/mathematics/glossary/glossary/ )
-
28 learning outcomes – click to view
Samples: Groups of 2. Groups of 3. Groups of 4. Groups of 5. Groups of 10. Counting on number line (by 2's).
-
Groups of two
- Activities: 4 course, 7 extra
-
-
- Groups of 2
- Tutorial
-
-
-
- Counting in two's - rows
- Practice
-
-
-
- Counting in two's - groups
- Practice
-
-
-
- Groups of 2
- Tutorial
-
Extra activities
-
-
- Groups of 2
- Printable
-
-
-
- Groups of 2
- Printable
-
-
-

- Groups of 2
- Practice
-
-
-

- Groups of 2
- Challenge
-
-
-

- Groups of 2
- Assessment
-
-
-

- Multiply by adding lots of 2
- Practice
-
-
Number patterns and groups (of 3)
- Activities: 3 course, 1 extra
-
-
- Groups of 3
- Tutorial
-
-
-
- Rows of 3
- Tutorial
-
-
-
- Groups of 3
- Practice
-
Extra activities
-
-

- Groups of three
- Practice
-
-
Groups and rows of 4
- Activities: 3 course, 4 extra
-
-
- Groups of 4
- Tutorial
-
-
-
- Rows of 4
- Tutorial
-
-
-
- Groups of 4
- Practice
-
Extra activities
-
-
- Groups of 4
- Tutorial
-
-
-
- Groups of four
- Printable
-
-
-
- Groups of four Answer sheet
- Printable
-
-
-

- Groups of four
- Practice
-
-
Groups of five
- Activities: 5 course, 14 extra
-
-
- Groups of 5
- Tutorial
-
-
-
- Rows of 5
- Practice
-
-
-
- Groups of 5
- Practice
-
-
-
- Groups of 5
- Tutorial
-
-
-
- Rows of 5
- Tutorial
-
Extra activities
-
-
- Groups of 5
- Printable
-
-
-
- Groups of 5
- Printable
-
-
-
- Groups of 5
- Printable
-
-
-
- Identifying the amounts in a group
- Tutorial
-
-
-
- Groups and rows of 5
- Tutorial
-
-
-
- Groups of 5
- Tutorial
-
-
-
- Rows of 5
- Tutorial
-
-
-

- Groups of 5
- Challenge
-
-
-

- Groups of 5
- Practice
-
-
-

- Multiply by adding lots of 5
- Practice
-
-
-

- Groups of 5
- Assessment
-
-
-

- Rows of five
- Practice
-
-
Groups of ten
- Activities: 6 course, 5 extra
-
-
- Groups of 10
- Tutorial
-
-
-
- Number of tens
- Practice
-
-
-
- Rows of 10
- Practice
-
-
-
- Groups of 10
- Practice
-
-
-
- Groups of 10
- Tutorial
-
-
-
- Rows Of 10
- Tutorial
-
Extra activities
-
-
- Groups of 10
- Printable
-
-
-
- Groups of 10
- Printable
-
-
-

- Groups of 10
- Challenge
-
-
-

- Rows of ten
- Practice
-
-
-

- Groups of 10
- Assessment
-
-
Counting on by two on a number line
- Activities: 7 course, 5 extra
-
-
- Counting on number line (by 2's)
- Tutorial
-
-
-
- Counting by 2
- Practice
-
-
-
- Counting by 2
- Practice
-
-
-
- Counting by 2
- Practice
-
-
-
- Counting by 2
- Tutorial
-
-
-
- Counting by 2
- Tutorial
-
-
-
- Counting by Two - Faster
- Tutorial
-
Extra activities
-
-
- Counting by 2
- Printable
-
-
-
- Counting by 2
- Tutorial
-
-
-

- Counting by 2
- Assessment
-
-
-

- Count on by 2 the next three numbers
- Practice
-
-
-

- Count by lots of 2
- Practice
-
-
Counting on by five on a number line
- Activities: 6 course, 3 extra
-
-
- Counting on number line (by 5's)
- Tutorial
-
-
-
- Counting by 5
- Tutorial
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Practice
-
-
-
- Counting by 5
- Tutorial
-
Extra activities
-
-
- Counting by 5
- Printable
-
-
-

- Counting by 5
- Assessment
-
-
-

- Count by lots of 5
- Practice
-
-
Counting on by ten on a number line
- Activities: 6 course, 5 extra
-
-
- Counting on number line (by 10's)
- Tutorial
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Practice
-
-
-
- Counting by 10
- Tutorial
-
-
-
- Counting by 10
- Tutorial
-
Extra activities
-
-
- Counting by 10
- Printable
-
-
-
- Counting by 10
- Printable
-
-
-

- Numbers Problem Solving
- Assessment
-
-
-

- Count by lots of 10
- Practice
-
-
-

- Counting by 10
- Assessment
-
-
Dividing by 2
- Activities: 4 course, 1 extra
-
-
- Dividing by 2
- Tutorial
-
-
-
- Dividing by 2
- Practice
-
-
-
- Dividing by 2
- Practice
-
-
-
- Dividing by 2
- Tutorial
-
Extra activities
-
-
- Dividing by 2
- Printable
-
-
2x tables (problem solving)
- Activities: 2 course, 7 extra
-
-
- 2x tables (problem solving)
- Practice
-
-
-
- 2x tables (problem solving)
- Practice
-
Extra activities
-
-
- 2x tables (problem solving)
- Printable
-
-
-
- 2x tables (problem solving)
- Printable
-
-
-
- 2x tables (problem solving)
- Printable
-
-
-
- 2x tables (problem solving)
- Printable
-
-
-
- 2x tables (problem solving)
- Printable
-
-
-
- 2x tables (problem solving) answer sheet
- Printable
-
-
-
- 2x tables (problem solving)
- Printable
-
-
3x tables (problem solving)
- Activities: 3 course, 3 extra
-
-
- 3x tables (problem solving)
- Practice
-
-
-
- 3x tables (problem solving)
- Practice
-
-
-
- 3x tables (problem solving)
- Practice
-
Extra activities
-
-
- 3x tables (problem solving)
- Printable
-
-
-
- 3x tables (problem solving)
- Printable
-
-
-
- 3x tables (problem solving)
- Printable
-
-
4x tables (problem solving)
- Activities: 3 course, 6 extra
-
-
- 4x tables (problem solving)
- Practice
-
-
-
- 4x tables (problem solving)
- Practice
-
-
-
- 4x tables (problem solving)
- Practice
-
Extra activities
-
-
- 4x tables (problem solving)
- Printable
-
-
-
- 4x tables (problem solving)
- Printable
-
-
-
- 4x tables (problem solving)
- Printable
-
-
-
- 4x tables (problem solving)
- Printable
-
-
-
- 4x tables (problem solving)
- Printable
-
-
-
- 4x tables (problem solving) answer sheet
- Printable
-
-
5x tables (problem solving)
- Activities: 2 course, 6 extra
-
-
- 5x tables (problem solving)
- Practice
-
-
-
- 5x tables (problem solving)
- Practice
-
Extra activities
-
-
- 5x tables (problem solving)
- Printable
-
-
-
- 5x tables (problem solving)
- Printable
-
-
-
- 5x tables (problem solving)
- Printable
-
-
-
- 5x tables (problem solving)
- Printable
-
-
-
- 5x tables (problem solving)
- Printable
-
-
-
- 5x tables (problem solving) answer sheet
- Printable
-
-
6x tables (problem solving)
- Activities: 2 course, 6 extra
-
-
- 6x tables (problem solving)
- Practice
-
-
-
- 6x tables (problem solving)
- Practice
-
Extra activities
-
-
- 6x tables (problem solving)
- Printable
-
-
-
- 6x tables (problem solving)
- Printable
-
-
-
- 6x tables (problem solving)
- Printable
-
-
-
- 6x tables (problem solving)
- Printable
-
-
-
- 6x tables (problem solving) Answer sheet
- Printable
-
-
-
- 6x tables (problem solving)
- Printable
-
-
7x tables (problem solving)
- Activities: 3 course, 6 extra
-
-
- 7x tables (problem solving)
- Practice
-
-
-
- 7x tables (problem solving)
- Practice
-
-
-
- 7x tables (problem solving)
- Practice
-
Extra activities
-
-
- 7x tables (problem solving)
- Printable
-
-
-
- 7x tables (problem solving)
- Printable
-
-
-
- 7x tables (problem solving)
- Printable
-
-
-
- 7x tables (problem solving)
- Printable
-
-
-
- 7x tables (problem solving) answer sheet
- Printable
-
-
-
- 7x tables (problem solving)
- Printable
-
-
8x tables (problem solving)
- Activities: 3 course, 5 extra
-
-
- 8x tables (problem solving)
- Practice
-
-
-
- 8x tables (problem solving)
- Practice
-
-
-
- 8x tables (problem solving)
- Practice
-
Extra activities
-
-
- 8x tables (problem solving)
- Printable
-
-
-
- 8x tables (problem solving)
- Printable
-
-
-
- 8x tables (problem solving)
- Printable
-
-
-
- 8x tables (problem solving)
- Printable
-
-
-
- 8x tables (problem solving)
- Printable
-
-
9x tables (problem solving)
- Activities: 3 course, 7 extra
-
-
- 9x tables (problem solving)
- Practice
-
-
-
- 9x tables (problem solving)
- Practice
-
-
-
- 9x tables (problem solving)
- Practice
-
Extra activities
-
-
- 9x tables (problem solving)
- Printable
-
-
-
- 9x tables (problem solving)
- Printable
-
-
-
- 9x tables (problem solving)
- Printable
-
-
-
- 9x tables (problem solving)
- Printable
-
-
-
- 9x tables (problem solving) answer sheet
- Printable
-
-
-
- 9x tables (problem solving) answer sheet
- Printable
-
-
-
- 9x tables (problem solving)
- Printable
-
-
10x tables (problem solving)
- Activities: 2 course, 6 extra
-
-
- 10x tables (problem solving)
- Practice
-
-
-
- 10x tables (problem solving)
- Practice
-
Extra activities
-
-
- 10x tables (problem solving)
- Printable
-
-
-
- 10x tables (problem solving)
- Printable
-
-
-
- 10x tables (problem solving)
- Printable
-
-
-
- 10x tables (problem solving)
- Printable
-
-
-
- 10x tables (problem solving)
- Printable
-
-
2x-10x tables (problem solving)
- Activities: 4 course, 9 extra
-
-
- 2x-10x tables (problem solving)
- Practice
-
-
-
- 2x-10x tables (problem solving)
- Practice
-
-
-
- 2x-10x tables (problem solving)
- Practice
-
-
-
- 2x-10x tables (problem solving)
- Practice
-
Extra activities
-
-
- Mixed tables (problem solving)
- Printable
-
-
-
- Mixed tables 2 (problem solving)
- Printable
-
-
-
- 2x-10x tables (problem solving)
- Printable
-
-
-
- 2x-10x tables (problem solving)
- Printable
-
-
-
- 2x-10x tables (problem solving)
- Printable
-
-
-
- 2x-10x tables (problem solving)
- Printable
-
-
-
- 2x-10x tables (problem solving)
- Printable
-
-
Dividing by 2 (problem solving)
- Activities: 2 course, 3 extra
-
-
- Dividing by 2 (problem solving)
- Practice
-
-
-
- Share between two - 2
- Practice
-
Extra activities
-
-
- Dividing by 2 (problem solving)
- Printable
-
-
-
- Dividing by 2 (problem solving)
- Printable
-
-
-
- Dividing by 2 (problem solving)
- Printable
-
-
Dividing by 3 (problem solving)
- Activities: 2 course, 2 extra
-
-
- Dividing by 3 (problem solving)
- Practice
-
-
-
- Dividing by 3
- Practice
-
Extra activities
-
-
- Dividing by 3 (problem solving)
- Printable
-
-
-
- Dividing by 3 (problem solving)
- Printable
-
-
Dividing by 6 (problem solving)
- Activities: 3 course, 4 extra
-
-
- Dividing by 6 (problem solving)
- Practice
-
-
-
- Dividing by 6 (problem solving)
- Practice
-
-
-
- Dividing by 6 - 2
- Practice
-
Extra activities
-
-
- Dividing by 6 (problem solving)
- Printable
-
-
-
- Dividing by 6
- Printable
-
-
-
- Dividing by 6 (problem solving)
- Printable
-
-
-
- Dividing by 6 - Answer sheet
- Printable
-
-
Dividing by 7 (problem solving)
- Activities: 4 course, 3 extra
-
-
- Dividing by 7 (problem solving)
- Practice
-
-
-
- Dividing by 7 (problem solving)
- Printable
-
-
-
- Dividing by 7 (problem solving)
- Practice
-
-
-
- Dividing by 7 (problem solving)
- Practice
-
Extra activities
-
-
- Dividing by 7 (problem solving)
- Printable
-
-
-
- Dividing by 7 (problem solving)
- Printable
-
-
Division facts (problem solving)
- Activities: 1 course, 6 extra
-
-
- Division facts (problem solving)
- Practice
-
Extra activities
-
-
- Two digit Division (no remainders)
- Printable
-
-
-
- Division Problem Solving
- Printable
-
-
-
- Division with no remainders
- Printable
-
-
-
- Division with no remainders
- Printable
-
-
-
28 learning outcomes – click to view
3.OA.4 – Determine the unknown whole number in a multiplication or division equation relating three whole numbers. For example, determine the unknown number that makes the equation true in each of the equations 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?
-
9 learning outcomes – click to view
Samples: 2x-10x tables (missing number). Identifying the dividend. Groups of 2. Groups of 5. Groups of 10. Groups of 3.
-
2x-10x tables (missing number)
- Activities: 3 course, 12 extra
-
-
- 2x-10x tables (missing number)
- Tutorial
-
-
-
- 2x-10x tables (missing number)
- Practice
-
-
-
- 2x-10x tables (missing number)
- Challenge
-
Extra activities
-
-
- 2x-10x tables (missing number)
- Printable
-
-
-
- 2x-10x tables (missing number)
- Printable
-
-
-
- 2x-10x tables (missing number)
- Printable
-
-
-
- 3967_ShortMultiplication_USA
- Tutorial
-
-
-
- 1X - 10X tables with a missing number
- Printable
-
-
-
- Drill - Tables - missing number
- Printable
-
-
-

- Times tables with a missing number
- Assessment
-
-
-

- Times tables - with a missing number
- Challenge
-
-
-

- 1X - 10X tables with a missing number
- Assessment
-
-
Dividing two-digits by one-digit (missing number)
- Activities: 3 course, 2 extra
-
-
- Identifying the dividend
- Practice
-
Extra activities
-
2x tables
- Activities: 12 course, 6 extra
-
-
- Groups of 2
- Tutorial
-
-
-
- Learning 2x tables
- Tutorial
-
-
-
- Number Patterns (2x tables)
- Practice
-
-
-
- 2x tables - matching answers
- Practice
-
-
-
- 2x tables
- Practice
-
-
-
- 2x tables (20 questions)
- Practice
-
-
-
- 2x tables
- Challenge
-
-
-
- 2x tables
- Tutorial
-
-
-
- Time tables match (2x)
- Practice
-
-
-
- 3x tables learn
- Practice
-
-
-
- 2x Tables
- Practice
-
-
-
- Test 2 X
- Practice
-
Extra activities
-
-
- 2x tables
- Printable
-
-
-
- Times Tables Chart
- Printable
-
-
-

- 2X tables
- Practice
-
-
-

- 2X tables
- Assessment
-
-
-

- Drill - 2X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 2X tables
- Printable
-
-
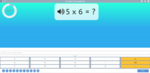
5x tables
- Activities: 9 course, 7 extra
-
-
- Groups of 5
- Tutorial
-
-
-
- Learning 5x tables
- Tutorial
-
-
-
- Number Patterns (5x tables)
- Practice
-
-
-
- 5x tables
- Practice
-
-
-
- 5x tables
- Practice
-
-
-
- 5x tables (20 questions)
- Practice
-
-
-
- 5x tables
- Challenge
-
-
-
- 5x tables
- Tutorial
-
-
-
- Counting by 5's on a clock face
- Tutorial
-
Extra activities
-
-
- 5x tables
- Printable
-
-
-
- 5x tables
- Printable
-
-
-
- 5x tables
- Printable
-
-
-

- 5X tables
- Practice
-
-
-

- Drill - 5X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 5X tables
- Printable
-
-
-

- 5X tables
- Assessment
-
-
10x tables
- Activities: 9 course, 6 extra
-
-
- Groups of 10
- Tutorial
-
-
-
- Learning 10x tables
- Tutorial
-
-
-
- Number Patterns (10x tables)
- Practice
-
-
-
- 10x tables
- Practice
-
-
-
- 10x tables
- Practice
-
-
-
- 10x tables (20 questions)
- Practice
-
-
-
- 10x tables
- Challenge
-
-
-
- 10x tables
- Printable
-
-
-
- 10x tables
- Tutorial
-
Extra activities
-
-
- 10x tables
- Printable
-
-
-
- 10x tables
- Printable
-
-
-

- 10 X Tables
- Practice
-
-
-

- Drill - 10X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 10X tables
- Printable
-
-
-

- 10X tables
- Assessment
-
-
3x tables
- Activities: 8 course, 8 extra
-
-
- Groups of 3
- Tutorial
-
-
-
- Learning 3x tables
- Tutorial
-
-
-
- Number Patterns (3x tables)
- Practice
-
-
-
- 3x tables
- Practice
-
-
-
- 3x tables
- Practice
-
-
-
- 3x tables (20 questions)
- Practice
-
-
-
- 3x tables
- Challenge
-
-
-
- 3x tables
- Tutorial
-
Extra activities
-
-
- 3x tables
- Printable
-
-
-
- Times tables chart
- Printable
-
-
-
- 3x tables
- Printable
-
-
-
- 3X tables
- Printable
-
-
-
- Drill - 3X tables
- Printable
-
-
-

- Drill - 3X tables (Auto-Generated)
- Printable
-
-
-

- 3X tables
- Assessment
-
-
4x tables
- Activities: 9 course, 6 extra
-
-
- Groups of 4
- Tutorial
-
-
-
- Learning 4x tables
- Tutorial
-
-
-
- Number Patterns (4x tables)
- Practice
-
-
-
- 4x tables
- Practice
-
-
-
- 4x tables
- Practice
-
-
-
- 4x tables (20 questions)
- Practice
-
-
-
- 4x tables
- Challenge
-
-
-
- 2x-5x tables
- Challenge
-
-
-
- 4x tables
- Tutorial
-
Extra activities
-
-
- 4x tables
- Printable
-
-
-
- 4X tables
- Printable
-
-
-

- 4X tables
- Assessment
-
-
-

- Drill - 4X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 4X tables
- Printable
-
-
Dividing by 3
- Activities: 4 course, 3 extra
-
-
- Dividing by 3
- Tutorial
-
-
-
- Dividing by 3
- Practice
-
-
-
- Share counters between three
- Practice
-
-
-
- Dividing by 3
- Tutorial
-
Extra activities
-
-
- Dividing by 3
- Printable
-
-
-
- Share counters between three
- Printable
-
-
Dividing by 4
- Activities: 4 course, 3 extra
-
-
- Dividing by 4
- Tutorial
-
-
-
- Dividing by 4
- Practice
-
-
-
- Dividing by 4
- Tutorial
-
-
-
- Share objects between four
- Printable
-
Extra activities
-
-
- Dividing by 4
- Printable
-
-
-
- Share objects between four
- Printable
-
-
-
- Share objects between four Answer sheet
- Printable
-
-
-
9 learning outcomes – click to view
Mathematics
3.OA.5 – Apply properties of operations as strategies to multiply and divide. (Students need not use formal terms for these properties.) Examples If 6 × 4 = 24 is known, then 4 × 6 = 24 is also known. (Commutative property of multiplication.) 3 × 5 × 2 can be found by 3 × 5 = 15, then 15 × 2 = 30, or by 5 × 2 = 10, then 3 × 10 = 30. (Associative property of multiplication.) Knowing that 8 × 5 = 40 and 8 × 2 = 16, one can find 8 × 7 as 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Distributive property.)
3.OA.6 – Understand division as an unknown-factor problem. For example, find 32 ÷ 8 by finding the number that makes 32 when multiplied by 8.
-
2 learning outcomes – click to view
Samples: Identifying the dividend. 2x-10x tables (missing number). Dividing two-digits by one-digit (missing number).
-
Dividing two-digits by one-digit (missing number)
- Activities: 3 course, 2 extra
-
-
- Identifying the dividend
- Practice
-
Extra activities
-
2x-10x tables (missing number)
- Activities: 3 course, 12 extra
-
-
- 2x-10x tables (missing number)
- Tutorial
-
-
-
- 2x-10x tables (missing number)
- Practice
-
-
-
- 2x-10x tables (missing number)
- Challenge
-
Extra activities
-
-
- 2x-10x tables (missing number)
- Printable
-
-
-
- 2x-10x tables (missing number)
- Printable
-
-
-
- 2x-10x tables (missing number)
- Printable
-
-
-
- 3967_ShortMultiplication_USA
- Tutorial
-
-
-
- 1X - 10X tables with a missing number
- Printable
-
-
-
- Drill - Tables - missing number
- Printable
-
-
-

- Times tables with a missing number
- Assessment
-
-
-

- Times tables - with a missing number
- Challenge
-
-
-

- 1X - 10X tables with a missing number
- Assessment
-
-
-
2 learning outcomes – click to view
Mathematics
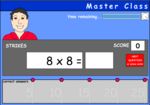
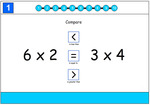
3.OA.7 – Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers.
-
19 learning outcomes – click to view
Samples: Groups of 2. Groups of 3. Challenge Puzzle - 3x tables. Groups of 4. 4x Multiplication facts - puzzle. Groups of 5.
-
2x tables
- Activities: 12 course, 6 extra
-
-
- Groups of 2
- Tutorial
-
-
-
- Learning 2x tables
- Tutorial
-
-
-
- Number Patterns (2x tables)
- Practice
-
-
-
- 2x tables - matching answers
- Practice
-
-
-
- 2x tables
- Practice
-
-
-
- 2x tables (20 questions)
- Practice
-
-
-
- 2x tables
- Challenge
-
-
-
- 2x tables
- Tutorial
-
-
-
- Time tables match (2x)
- Practice
-
-
-
- 3x tables learn
- Practice
-
-
-
- 2x Tables
- Practice
-
-
-
- Test 2 X
- Practice
-
Extra activities
-
-
- 2x tables
- Printable
-
-
-
- Times Tables Chart
- Printable
-
-
-

- 2X tables
- Practice
-
-
-

- 2X tables
- Assessment
-
-
-

- Drill - 2X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 2X tables
- Printable
-
-
3x tables
- Activities: 8 course, 8 extra
-
-
- Groups of 3
- Tutorial
-
-
-
- Learning 3x tables
- Tutorial
-
-
-
- Number Patterns (3x tables)
- Practice
-
-
-
- 3x tables
- Practice
-
-
-
- 3x tables
- Practice
-
-
-
- 3x tables (20 questions)
- Practice
-
-
-
- 3x tables
- Challenge
-
-
-
- 3x tables
- Tutorial
-
Extra activities
-
-
- 3x tables
- Printable
-
-
-
- Times tables chart
- Printable
-
-
-
- 3x tables
- Printable
-
-
-
- 3X tables
- Printable
-
-
-
- Drill - 3X tables
- Printable
-
-
-

- Drill - 3X tables (Auto-Generated)
- Printable
-
-
-

- 3X tables
- Assessment
-
-
4x tables
- Activities: 9 course, 6 extra
-
-
- Groups of 4
- Tutorial
-
-
-
- Learning 4x tables
- Tutorial
-
-
-
- Number Patterns (4x tables)
- Practice
-
-
-
- 4x tables
- Practice
-
-
-
- 4x tables
- Practice
-
-
-
- 4x tables (20 questions)
- Practice
-
-
-
- 4x tables
- Challenge
-
-
-
- 2x-5x tables
- Challenge
-
-
-
- 4x tables
- Tutorial
-
Extra activities
-
-
- 4x tables
- Printable
-
-
-
- 4X tables
- Printable
-
-
-

- 4X tables
- Assessment
-
-
-

- Drill - 4X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 4X tables
- Printable
-
-
5x tables
- Activities: 9 course, 7 extra
-
-
- Groups of 5
- Tutorial
-
-
-
- Learning 5x tables
- Tutorial
-
-
-
- Number Patterns (5x tables)
- Practice
-
-
-
- 5x tables
- Practice
-
-
-
- 5x tables
- Practice
-
-
-
- 5x tables (20 questions)
- Practice
-
-
-
- 5x tables
- Challenge
-
-
-
- 5x tables
- Tutorial
-
-
-
- Counting by 5's on a clock face
- Tutorial
-
Extra activities
-
-
- 5x tables
- Printable
-
-
-
- 5x tables
- Printable
-
-
-
- 5x tables
- Printable
-
-
-

- 5X tables
- Practice
-
-
-

- Drill - 5X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 5X tables
- Printable
-
-
-

- 5X tables
- Assessment
-
-
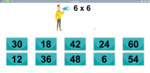
6x tables
- Activities: 7 course, 4 extra
-
-
- Learning 6x tables
- Tutorial
-
-
-
- Number Patterns (6x tables)
- Practice
-
-
-
- 6x tables
- Practice
-
-
-
- 6x tables
- Practice
-
-
-
- 6x tables (20 questions)
- Practice
-
-
-
- 6x tables
- Challenge
-
-
-
- 6x tables
- Tutorial
-
Extra activities
-
-
- 6x tables
- Printable
-
-
-

- Drill 6X tables (Auto-Generated)
- Printable
-
-
-
- Drill 6X tables
- Printable
-
-
-

- 6X tables
- Assessment
-
-
7x tables
- Activities: 7 course, 5 extra
-
-
- Learning 7x tables
- Tutorial
-
-
-
- Number Patterns (7x tables)
- Practice
-
-
-
- 7x tables
- Practice
-
-
-
- 7x tables
- Practice
-
-
-
- 7x tables (20 questions)
- Practice
-
-
-
- 7x tables
- Challenge
-
-
-
- 7x tables
- Tutorial
-
Extra activities
-
-
- 7x tables
- Printable
-
-
-

- Drill - 7X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 7X tables
- Printable
-
-
-
- 7X tables
- Printable
-
-
-

- 7X tables
- Assessment
-
-
8x tables
- Activities: 7 course, 5 extra
-
-
- Learning 8x tables
- Tutorial
-
-
-
- Number Patterns (8x tables)
- Practice
-
-
-
- 8x tables
- Practice
-
-
-
- 8x tables
- Practice
-
-
-
- 8x tables (20 questions)
- Practice
-
-
-
- 8x tables
- Challenge
-
-
-
- 8x tables
- Tutorial
-
Extra activities
-
-
- 8x tables
- Printable
-
-
-

- Drill - 8X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 8X tables
- Printable
-
-
-

- 8X tables
- Assessment
-
-
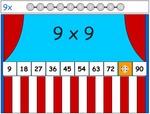
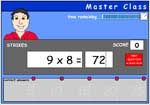
9x tables
- Activities: 7 course, 6 extra
-
-
- Learning 9x tables
- Tutorial
-
-
-
- Number Patterns (9x tables)
- Practice
-
-
-
- 9x tables
- Practice
-
-
-
- 9x tables
- Practice
-
-
-
- 9x tables (20 questions)
- Practice
-
-
-
- 9x tables
- Challenge
-
-
-
- 9x tables
- Tutorial
-
Extra activities
-
-
- 9x tables
- Printable
-
-
-
- 8X and 9X tables
- Printable
-
-
-

- Drill - 9X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 9X tables
- Printable
-
-
-

- 9X tables
- Assessment
-
-
2x-10x tables
- Activities: 5 course, 12 extra
-
-
- Tricky 20
- Practice
-
-
-
- 2x-10x tables
- Practice
-
-
-
- 2x-10x tables
- Challenge
-
-
-
- Times Tables Test (25 questions)
- Practice
-
-
-
- Matching facts - Concentration Game
- Practice
-
Extra activities
-
-
- Multiplication table
- Printable
-
-
-
- 2x-10x tables
- Printable
-
-
-
- 2x-10x tables
- Printable
-
-
-
- 2x-10x tables
- Printable
-
-
-

- Comparing multiplication facts
- Practice
-
-
-

- Matching multiplication facts
- Practice
-
-
-

- Multiplication Problem Solving
- Practice
-
-
-

- Drill - 1X - 10X tables (Auto-Generated)
- Printable
-
-
-
- Drill - 1X - 10X tables
- Printable
-
-
-

- Tables 1x - 10x (Auto-Generated)
- Printable
-
-
-

- Times Tables 1x-10x
- Practice
-
-
-

- 1x-10x tables
- Assessment
-
-
Dividing by 3
- Activities: 4 course, 3 extra
-
-
- Dividing by 3
- Tutorial
-
-
-
- Dividing by 3
- Practice
-
-
-
- Share counters between three
- Practice
-
-
-
- Dividing by 3
- Tutorial
-
Extra activities
-
-
- Dividing by 3
- Printable
-
-
-
- Share counters between three
- Printable
-
-
Dividing by 4
- Activities: 4 course, 3 extra
-
-
- Dividing by 4
- Tutorial
-
-
-
- Dividing by 4
- Practice
-
-
-
- Dividing by 4
- Tutorial
-
-
-
- Share objects between four
- Printable
-
Extra activities
-
-
- Dividing by 4
- Printable
-
-
-
- Share objects between four
- Printable
-
-
-
- Share objects between four Answer sheet
- Printable
-
-
Dividing by 6
- Activities: 2 course, 1 extra
-
Dividing by 7
- Activities: 2 course, 1 extra
-
Dividing by 8
- Activities: 2 course, 1 extra
-
Dividing by 9
- Activities: 1 course, 1 extra
-
2x-10x tables - puzzle
- Activities: 1 course, 0 extra
-
Dividing two-digits by one-digit (no remainders)
- Activities: 7 course, 9 extra
-
-
- Dividing two-digits by one-digit
- Practice
-
-
-
- Division facts
- Challenge
-
-
-
- Division with no remainders
- Tutorial
-
Extra activities
-
-
- Dividing two-digits by one-digit
- Printable
-
-
-
- Drill - Division - no remainders
- Printable
-
-
-
- Share 12 using division symbol
- Tutorial
-
-
-

- Division with no remainders
- Practice
-
-
-

- Share 12
- Practice
-
-
-

- Division with no remainders
- Practice
-
-
-

- Division with no remainders
- Assessment
-
-
-
19 learning outcomes – click to view
Mathematics
3.OA.8 – Solve two-step word problems using the four operations. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding. (This standard is limited to problems posed with whole numbers and having whole-number answers; students should know how to perform operations in the conventional order when there are no parentheses to specify a particular order.)
-
5 learning outcomes – click to view
Samples: Subtraction (two step problem solving). Represent problems using algebraic equation. Two step problem solving.
-
Subtraction (two step problem solving)
- Activities: 2 course, 1 extra
-
Represent problems using algebraic equation
- Activities: 1 course, 0 extra
-
Two step problem solving
- Activities: 1 course, 1 extra
-
-
- Two step problem solving
- Practice
-
Extra activities
-
-
5 learning outcomes – click to view
3.OA.9 – Identify arithmetic patterns (including patterns in the addition table or multiplication table), and explain them using properties of operations. For example, observe that 4 times a number is always even, and explain why 4 times a number can be decomposed into two equal addends.
-
9 learning outcomes – click to view
Samples: Groups of 6. Rows of 7. Groups of 8. Groups of 9. Number Patterns (2,3,5,10).
-
Number Patterns (2,3,5,10)
- Activities: 2 course, 5 extra
-
-
- Number Patterns (2,3,5,10)
- Practice
-
-
-
- Missing elements in number patterns
- Practice
-
Extra activities
-
-
- Patterns Problem Solving
- Printable
-
-
-
- Patterns and algebra
- Printable
-
-
-

- Patterns and algebra
- Assessment
-
-
-

- Patterns Problem Solving
- Assessment
-
-
Representing word problems as number sentences
- Activities: 1 course, 0 extra
-
Continue number patterns resulting from addition or subtraction
- Activities: 1 course, 1 extra
-
-
- Continue number patterns
- Practice
-
Extra activities
-
Shapes Algebra
- Activities: 2 course, 0 extra
-
-
- Shapes Algebra
- Practice
-
-
-
- Challenge puzzle - Algebra
- Practice
-
-
9 learning outcomes – click to view
3.NBT – Number & Operations in Base Ten
Mathematics
3.NBT.1 – Use place value understanding to round whole numbers to the nearest 10 or 100.
-
2 learning outcomes – click to view
Samples: Rounding to the nearest 10 (3 digits). Rounding to the nearest hundred. Rounding numbers: Activity 2.
-
Rounding to the nearest 10
- Activities: 3 course, 3 extra
-
-
- Rounding numbers: Activity 2
- Practice
-
-
-
- Rounding numbers: Activity 4
- Practice
-
Extra activities
-
-
- Rounding numbers
- Printable
-
-
-
- Rounding numbers Answer sheet
- Printable
-
-
Rounding to the nearest hundred
- Activities: 3 course, 0 extra
-
-
- Rounding to the nearest hundred
- Practice
-
-
-
- Rounding to the nearest hundred
- Practice
-
-
-
2 learning outcomes – click to view
3.NBT.2 – Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
-
7 learning outcomes – click to view
Samples: Adding three digit numbers using blocks. Subtracting 10 large numbers. Subtracting 100.
-
Place value - adding three-digit numbers
- Activities: 2 course, 0 extra
-
Subtracting 10 from larger numbers
- Activities: 1 course, 1 extra
-
Subtracting 100 from larger numbers
- Activities: 1 course, 1 extra
-
Place value - subtracting three-digit numbers
- Activities: 1 course, 0 extra
-
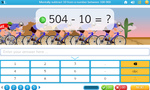
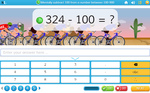
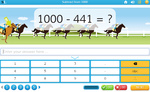
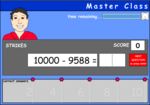
Subtracting from 1000
- Activities: 6 course, 10 extra
-
-
- Subtracting from 1000
- Practice
-
-
-
- Subtract from lots of 10,000
- Tutorial
-
-
-
- Subtracting from 1000
- Tutorial
-
Extra activities
-
-
- Subtracting from 1000
- Printable
-
-
-
- Subtracting from 1000 (problem solving)
- Printable
-
-
-
- Subtracting from 1000 (problem solving)
- Printable
-
-
-

- Subtracting from lots of 1000
- Practice
-
-
-

- Subtract from 10,000
- Challenge
-
-
-

- Subtract from 10,000
- Assessment
-
-
-

- Subtract from lots of 10,000
- Practice
-
-
-

- Subtracting from lots of 1000
- Challenge
-
-
-

- Subtracting from lots of 1000
- Assessment
-
-
-
- Subtracting from lots of 1000
- Tutorial
-
-
Subtraction - missing number
- Activities: 1 course, 2 extra
-
Subtraction and addition (problem solving)
- Activities: 1 course, 1 extra
Extra activities
-
-
- Subtraction and addition
- Printable
-
-
-
7 learning outcomes – click to view
3.NBT.3 – Multiply one-digit whole numbers by multiples of 10 in the range 10–90 (e.g., 9 × 80, 5 × 60) using strategies based on place value and properties of operations.
-
4 learning outcomes – click to view
Samples: Multiplying multiples of 10 by a single digit. Challenge Puzzle. Short multiplication of multiples of 10.
-
Multiplying a single-digit number by multiples of 10
- Activities: 8 course, 5 extra
-
-
- Multiplying multiples of 10
- Practice
-
-
-
- Multiplying multiples of 10
- Practice
-
-
-
- Multiplying multiples of 10
- Practice
-
-
-
- Multiplying multiples of 10
- Challenge
-
-
-
- Multiplying multiples of 10
- Tutorial
-
-
-
- Multiplying multiples of 10
- Tutorial
-
Extra activities
-
-
- Multiplying multiples of 10
- Printable
-
-
-

- Short multiplication of multiples of 10
- Assessment
-
-
Multiples of 10 by 1 digit - problem solving
- Activities: 0 course, 1 extra
Extra activities
-
-
- Short multiplication of multiples of 10
- Printable
-
-
Multiplying a two-digit number by a one-digit number - problem solving
- Activities: 4 course, 8 extra
Extra activities
-
-

- Multiplying 2 digits by a 1 digit number
- Assessment
-
-
-

- Multiplying 2 digits by a 1 digit number
- Assessment
-
-
-
- Short multiplication
- Printable
-
-
-
4 learning outcomes – click to view
3.NF – Number & Operations—Fractions¹ (Grade 3 expectations in this domain are limited to fractions with denominators 2, 3, 4, 6, 8.)
Mathematics
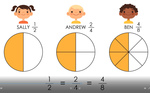
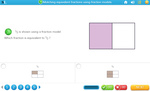
3.NF.1 – Understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b.
-
6 learning outcomes – click to view
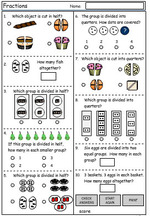
Samples: A half. Halving groups. Representing fractions. Writing fractions. Counting on - fractions. A half. Halving groups.
-
Halving objects
- Activities: 4 course, 3 extra
-
-
- A half
- Tutorial
-
-
-
- A half
- Practice
-
-
-
- Recognizing halves
- Printable
-
-
-
- Halves and quarters
- Tutorial
-
Extra activities
-
-
- Matching halves
- Printable
-
-
-

- Halves - identifying an equal share
- Practice
-
-
-
- fractions test
- Practice
-
-
Halving groups
- Activities: 3 course, 1 extra
-
-
- Halving groups
- Tutorial
-
-
-
- Halving groups
- Practice
-
-
-
- Halves: identifying an equal share
- Tutorial
-
Extra activities
-
-
- Halving groups
- Printable
-
-
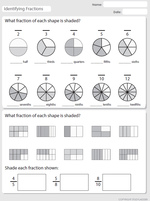
Identifying fractions
- Activities: 6 course, 4 extra
-
-
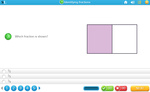
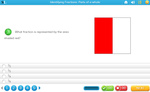
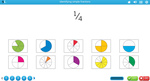
- Writing fractions
- Tutorial
-
-
-
- Identifying fractions
- Practice
-
-
-
- Identifying fractions
- Practice
-
-
-
- Identifying simple fractions
- Practice
-
-
-
- Fractions Chart
- Printable
-
-
-
- Identifying Fractions
- Tutorial
-
Extra activities
-
-
- Representing fractions
- Printable
-
-
-
- Identifying fractions
- Printable
-
-
-
- Identifying fractions tutorial
- Tutorial
-
-
-

- Identifying fractions
- Practice
-
-
-
6 learning outcomes – click to view
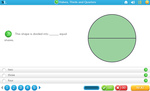
3.NF.2 – Understand a fraction as a number on the number line; represent fractions on a number line diagram.
3.NF.2.a – Represent a fraction 1/b on a number line diagram by defining the interval from 0 to 1 as the whole and partitioning it into b equal parts. Recognize that each part has size 1/b and that the endpoint of the part based at 0 locates the number 1/b on the number line.
-
1 learning outcomes – click to view
Samples: Fractions on a number line. Fractions on a number line (with guides). Fractions on a number line.
-
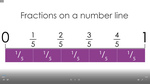
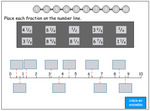
Fractions on a number line.
- Activities: 4 course, 1 extra
-
-
- Fractions on a number line.
- Tutorial
-
-
-
- Fractions on a number line
- Practice
-
-
-
- Placing fractions on a number line
- Practice
-
Extra activities
-
-

- Fractions on a Number Line
- Practice
-
-
-
1 learning outcomes – click to view
3.NF.2.b – Represent a fraction a/b on a number line diagram by marking off a lengths 1/b from 0. Recognize that the resulting interval has size a/b and that its endpoint locates the number a/b on the number line.
-
1 learning outcomes – click to view
Samples: Fractions on a number line. Fractions on a number line (with guides). Fractions on a number line.
-
Fractions on a number line.
- Activities: 4 course, 1 extra
-
-
- Fractions on a number line.
- Tutorial
-
-
-
- Fractions on a number line
- Practice
-
-
-
- Placing fractions on a number line
- Practice
-
Extra activities
-
-

- Fractions on a Number Line
- Practice
-
-
-
1 learning outcomes – click to view
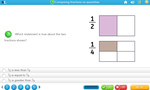
3.NF.3 – Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
3.NF.3.a – Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
-
4 learning outcomes – click to view
Samples: Modelling equivalent fractions. Equivalent Fractions. Hundredths in their lowest forms.
-
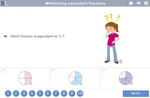
Modelling equivalent fractions
- Activities: 4 course, 3 extra
-
-
- Modelling equivalent fractions
- Practice
-
-
-
- Matching equivalent fractions
- Practice
-
-
-
- Equivalence
- Tutorial
-
-
-
- Modelling equivalent fractions
- Practice
-
Extra activities
-
Hundredths in their lowest forms
- Activities: 1 course, 0 extra
-
-
- Hundredths in their lowest forms
- Practice
-
-
Comparing fractions as quantities.
- Activities: 1 course, 0 extra
-
-
- Comparing fractions as quantities
- Practice
-
-
-
4 learning outcomes – click to view
3.NF.3.b – Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3). Explain why the fractions are equivalent, e.g., by using a visual fraction model.
-
2 learning outcomes – click to view
Samples: Equivalent Fractions. Modelling equivalent fractions. Matching equivalent fractions using fraction models.
-
Modelling equivalent fractions
- Activities: 4 course, 3 extra
-
-
- Modelling equivalent fractions
- Practice
-
-
-
- Matching equivalent fractions
- Practice
-
-
-
- Equivalence
- Tutorial
-
-
-
- Modelling equivalent fractions
- Practice
-
Extra activities
-
2 learning outcomes – click to view
3.NF.3.c – Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram.
-
10 learning outcomes – click to view
Samples: Introduction to Fractions. Quarters. Fractions of groups. Representing fractions. Writing fractions.
-
Halves, thirds and quarters
- Activities: 2 course, 1 extra
-
-
- Introduction to Fractions
- Tutorial
-
-
-
- Halves, thirds and quarters
- Practice
-
Extra activities
-
-
- Thirds
- Printable
-
-
Halves, quarters and eighths
- Activities: 7 course, 10 extra
-
-
- Quarters
- Tutorial
-
-
-
- Eighths
- Tutorial
-
-
-
- Halves and Quarters
- Practice
-
-
-
- Halves and quarters
- Tutorial
-
-
-
- Identifying Fractions
- Tutorial
-
Extra activities
-
-
- Quarters and eighths
- Printable
-
-
-
- Identifying fractions tutorial
- Tutorial
-
-
-
- Halves and quarters tutorial
- Tutorial
-
-
-
- Fraction of objects and shapes
- Practice
-
-
-

- Compare to a half tutorial
- Tutorial
-
-
-

- Compare to a half
- Practice
-
-
-

- Comparing fractions tutorial
- Tutorial
-
-
-
- Identifying halves and quarters
- Practice
-
-
-

- Comparing fractions
- Practice
-
-
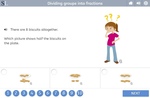
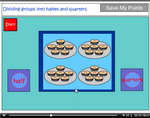
Dividing groups into halves and quarters
- Activities: 5 course, 5 extra
-
-
- Fractions of groups
- Tutorial
-
-
-
- Dividing groups into fractions
- Practice
-
-
-
- Fraction- Groups
- Printable
-
Extra activities
-
-
- Fractions
- Printable
-
-
-
- Fractions Problem Solving
- Printable
-
-
-

- Fractions
- Assessment
-
-
-

- Fractions Problem Solving
- Assessment
-
-
Identifying fractions
- Activities: 6 course, 4 extra
-
-
- Writing fractions
- Tutorial
-
-
-
- Identifying fractions
- Practice
-
-
-
- Identifying fractions
- Practice
-
-
-
- Identifying simple fractions
- Practice
-
-
-
- Fractions Chart
- Printable
-
-
-
- Identifying Fractions
- Tutorial
-
Extra activities
-
-
- Representing fractions
- Printable
-
-
-
- Identifying fractions
- Printable
-
-
-
- Identifying fractions tutorial
- Tutorial
-
-
-

- Identifying fractions
- Practice
-
-
Comparing fractions as quantities.
- Activities: 1 course, 0 extra
-
-
- Comparing fractions as quantities
- Practice
-
-
Modelling equivalent fractions
- Activities: 4 course, 3 extra
-
-
- Modelling equivalent fractions
- Practice
-
-
-
- Matching equivalent fractions
- Practice
-
-
-
- Equivalence
- Tutorial
-
-
-
- Modelling equivalent fractions
- Practice
-
Extra activities
-
Comparing fractions to one whole
- Activities: 1 course, 0 extra
-
-
- Comparing fractions - 1 whole
- Practice
-
-
-
10 learning outcomes – click to view
3.NF.3.d – Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
-
2 learning outcomes – click to view
Samples: Comparing fractions as quantities. Modelling equivalent fractions. Matching equivalent fractions. Equivalence.
-
Comparing fractions as quantities.
- Activities: 1 course, 0 extra
-
-
- Comparing fractions as quantities
- Practice
-
-
Modelling equivalent fractions
- Activities: 4 course, 3 extra
-
-
- Modelling equivalent fractions
- Practice
-
-
-
- Matching equivalent fractions
- Practice
-
-
-
- Equivalence
- Tutorial
-
-
-
- Modelling equivalent fractions
- Practice
-
Extra activities
-
-
2 learning outcomes – click to view
3.MD – Measurement & Data
Mathematics
3.MD.1 – Tell and write time to the nearest minute and measure time intervals in minutes. Solve word problems involving addition and subtraction of time intervals in minutes, e.g., by representing the problem on a number line diagram.
-
5 learning outcomes – click to view
Samples: Estimate the duration of time. Months of the Year. Reading a Calendar. Timelines. Telling the time.
-
Most likely duration for an event
- Activities: 1 course, 2 extra
-
-
- Estimate the duration of time.
- Practice
-
Extra activities
-
Months of the Year
- Activities: 1 course, 3 extra
-
-
- Months of the Year
- Practice
-
Extra activities
-
-
- Time
- Printable
-
-
-
- Time
- Printable
-
-
-

- Months of the year
- Practice
-
-
Reading a Calendar
- Activities: 2 course, 5 extra
-
-
- Reading a Calendar
- Tutorial
-
-
-
- Reading a Calendar
- Practice
-
Extra activities
-
-
- Reading a Calendar
- Practice
-
-
-
- Reading calendars: Activity 2
- Practice
-
-
-

- Time Problem Solving
- Assessment
-
-
-
- Time Problem Solving
- Printable
-
-
-

- Reading a calendar
- Practice
-
-
Timelines
- Activities: 1 course, 5 extra
-
-
- Timelines
- Practice
-
Extra activities
-
-
- Timelines: Activity 1
- Practice
-
-
-
- Timelines: Activity 2
- Practice
-
-
-

- Time Problem Solving
- Assessment
-
-
-

- Reading a timeline
- Practice
-
-
Reading Time - to the minute
- Activities: 4 course, 9 extra
-
-
- Telling the time
- Tutorial
-
-
-
- Reading Five Minute Intervals
- Tutorial
-
-
-
- Tell time to the minute
- Practice
-
-
-
- Reading Time - to the minute
- Practice
-
Extra activities
-
-
- Tell time to the minute: Activity 2
- Practice
-
-
-

- Telling the time
- Practice
-
-
-

- Telling the time
- Practice
-
-
-
- Reading analog to one minute intervals
- Printable
-
-
-
- Recording analog time in digital format
- Printable
-
-
-
- Time
- Printable
-
-
-

- Time
- Assessment
-
-
-
5 learning outcomes – click to view
3.MD.2 – Measure and estimate liquid volumes and masses of objects using standard units of grams (g), kilograms (kg), and liters (l). (Excludes multiplicative comparison problems (problems involving notions of “times as much”; see Glossary, Table 2 http://www.corestandards.org/the-standards/mathematics/glossary/glossary/ ). Add, subtract, multiply, or divide to solve one-step word problems involving masses or volumes that are given in the same units, e.g., by using drawings (such as a beaker with a measurement scale) to represent the problem. (Excludes compound units such as cm3 and finding the geometric volume of a container.)
-
8 learning outcomes – click to view
Samples: Comparing volume (empty to full). Measuring capacity using informal units tutorial.
-
Full to empty
- Activities: 3 course, 1 extra
-
-
- Comparing volume (empty to full)
- Tutorial
-
-
-
- Full to empty
- Practice
-
-
-
- Comparing Capacity
- Tutorial
-
Extra activities
-
Direct comparison - volume
- Activities: 1 course, 4 extra
Extra activities
-
-

- Compare capacity of two containers
- Practice
-
-
Volume using informal units
- Activities: 3 course, 10 extra
-
-
- Measure volume using informal units
- Practice
-
-
-
- Comparing volume
- Printable
-
Extra activities
-
-
- Volume Problem Solving
- Printable
-
-
-
- Volume
- Printable
-
-
-

- Volume Problem Solving
- Assessment
-
-
-

- Volume
- Assessment
-
-
Objects using cubes
- Activities: 3 course, 5 extra
-
-
- Objects using cubes
- Tutorial
-
-
-
- Objects using cubes
- Practice
-
-
-
- Objects using cubes
- Tutorial
-
Extra activities
-
-
- Compare the volume of two stacks
- Tutorial
-
-
-

- Comparing the volume of two stacks
- Practice
-
-
Measure volume using litres and milliltres
- Activities: 1 course, 2 extra
-
-
- Millilitres And Litres
- Tutorial
-
Extra activities
-
Measure mass in grams and kilograms
- Activities: 1 course, 11 extra
Extra activities
-
-

- Measuring using grams and kilograms
- Tutorial
-
-
-

- Mass Problem Solving
- Assessment
-
-
-

- Measuring weight in grams (g)
- Practice
-
-
Compare mass using a balance scale
- Activities: 4 course, 2 extra
-
-
- Compare mass using a balance scale
- Tutorial
-
-
-
- Compare mass using a balance scale
- Practice
-
-
-
- Comparing the mass of two objects
- Tutorial
-
-
-
- Ordering Mass lightest heaviest_USA
- Tutorial
-
Extra activities
-
-

- Comparing mass using a balance
- Practice
-
-
Measure mass with informal units
- Activities: 6 course, 7 extra
-
-
- Measuring mass using informal units
- Tutorial
-
-
-
- Measuring mass using informal units
- Tutorial
-
Extra activities
-
-
- Mass
- Printable
-
-
-

- Mass Problem Solving
- Assessment
-
-
-

- Mass
- Assessment
-
-
-

- Measuring mass using informal units
- Practice
-
-
-

- Comparing mass using informal units
- Practice
-
-
-
8 learning outcomes – click to view
Mathematics
3.MD.3 – Draw a scaled picture graph and a scaled bar graph to represent a data set with several categories. Solve one- and two-step “how many more” and “how many less” problems using information presented in scaled bar graphs. For example, draw a bar graph in which each square in the bar graph might represent 5 pets.
-
6 learning outcomes – click to view
Samples: Data tables. Data - tally marks. Interpret data in lists. Data - picture graphs. Create a Column Graph. Data.
-
Interpret data presented in a table
- Activities: 3 course, 3 extra
-
-
- Data tables
- Practice
-
-
-
- Reading tables.
- Practice
-
-
-
- Data in tables: Activity 2
- Practice
-
Extra activities
-
-
- Display data in a table
- Printable
-
-
-

- Recording information in a table
- Practice
-
-
Interpret data presented with tally marks
- Activities: 2 course, 2 extra
-
-
- Data - tally marks
- Practice
-
-
-
- Data - tally marks: Activity 2
- Practice
-
Extra activities
-
-
- Display data using tally marks
- Printable
-
-
-

- Reading tally marks
- Practice
-
-
Interpret data presented using picture graphs.
- Activities: 2 course, 4 extra
-
-
- Data - picture graphs
- Practice
-
-
-
- Picture graphs.
- Practice
-
Extra activities
-
-
- Display data using picture graphs
- Printable
-
-
-
- Data - picture graphs: Activity 2
- Practice
-
-
-

- Reading picture graphs
- Practice
-
-
-

- Making picture graphs
- Practice
-
-
Data & Graphs - Column Graph Creator
- Activities: 0 course, 1 extra
Extra activities
-
-

- Create a Column Graph
- Whiteboard
-
-
Interpret data presented using simple column graphs
- Activities: 0 course, 6 extra
Extra activities
-
-

- Data
- Assessment
-
-
-

- Data
- Assessment
-
-
-

- Data Problem Solving
- Assessment
-
-
-

- Data Problem Solving
- Assessment
-
-
-

- Making a bar graph
- Practice
-
-
-

- Reading a column graph
- Practice
-
-
-
6 learning outcomes – click to view
3.MD.4 – Generate measurement data by measuring lengths using rulers marked with halves and fourths of an inch. Show the data by making a line plot, where the horizontal scale is marked off in appropriate units— whole numbers, halves, or quarters.
Mathematics
3.MD.5 – Recognize area as an attribute of plane figures and understand concepts of area measurement.
3.MD.5.a – A square with side length 1 unit, called “a unit square,” is said to have “one square unit” of area, and can be used to measure area.
-
2 learning outcomes – click to view
Samples: Counting by using rows. Area using square tiles. Counting by using rows. Partitioned rectangles.
-
Partitioned rectangles
- Activities: 3 course, 0 extra
-
-
- Counting by using rows
- Tutorial
-
-
-
- Counting by using rows
- Tutorial
-
-
-
- Partitioned rectangles
- Practice
-
-
-
2 learning outcomes – click to view
3.MD.5.b – A plane figure which can be covered without gaps or overlaps by n unit squares is said to have an area of n square units.
-
2 learning outcomes – click to view
Samples: Area using informal units. Counting by using rows. Area using informal units. Counting by using rows.
-
Area using informal units.
- Activities: 2 course, 5 extra
-
-
- Area using informal units
- Tutorial
-
-
-
- Area using informal units
- Practice
-
Extra activities
-
-

- Calculate Area Using Informal Units
- Whiteboard
-
-
-

- Measure area using informal units
- Practice
-
-
Partitioned rectangles
- Activities: 3 course, 0 extra
-
-
- Counting by using rows
- Tutorial
-
-
-
- Counting by using rows
- Tutorial
-
-
-
- Partitioned rectangles
- Practice
-
-
-
2 learning outcomes – click to view
3.MD.6 – Measure areas by counting unit squares (square cm, square m, square in, square ft, and improvised units).
-
1 learning outcomes – click to view
Samples: Measure using square centimeters. Measure using square centimetres. Measure area using a grid tutorial.
-
Area using a grid.
- Activities: 4 course, 11 extra
-
-
- Measure using square centimeters
- Tutorial
-
-
-
- Measure using square centimetres
- Tutorial
-
-
-
- Measure area using a grid tutorial
- Tutorial
-
Extra activities
-
-
- Drawing shapes that have a given area.
- Printable
-
-
-

- Compare area tutorial
- Tutorial
-
-
-

- Measuring area using informal units
- Practice
-
-
-

- Compare area
- Practice
-
-
-

- Measure area using a grid
- Practice
-
-
-

- Calculating area using a grid
- Practice
-
-
-
1 learning outcomes – click to view
3.MD.7 – Relate area to the operations of multiplication and addition.
3.MD.7.a – Find the area of a rectangle with whole-number side lengths by tiling it, and show that the area is the same as would be found by multiplying the side lengths.
-
2 learning outcomes – click to view
Samples: Counting by using rows. Area using square tiles. Counting by using rows. Partitioned rectangles.
-
Partitioned rectangles
- Activities: 3 course, 0 extra
-
-
- Counting by using rows
- Tutorial
-
-
-
- Counting by using rows
- Tutorial
-
-
-
- Partitioned rectangles
- Practice
-
-
-
2 learning outcomes – click to view
3.MD.7.b – Multiply side lengths to find areas of rectangles with whole-number side lengths in the context of solving real world and mathematical problems, and represent whole-number products as rectangular areas in mathematical reasoning.
-
1 learning outcomes – click to view
Samples: Calculating area. Area of Squares and Rectangles. Calculating the area of squares and rectangles. Calculating Area.
-
Calculating area (squares and rectangles)
- Activities: 5 course, 8 extra
-
-
- Calculating area
- Tutorial
-
-
-
- Area of Squares and Rectangles
- Practice
-
-
-
- Calculating Area
- Tutorial
-
-
-
- Calculating area using a grid
- Tutorial
-
Extra activities
-
-
- Calculating area in square centimetres
- Printable
-
-
-
- Area match - squares and rectangles
- Practice
-
-
-

- Arrays
- Practice
-
-
-

- Using A Calculator to Work Out Area
- Practice
-
-
-
1 learning outcomes – click to view
3.MD.7.c – Use tiling to show in a concrete case that the area of a rectangle with whole-number side lengths a and b + c is the sum of a × b and a × c. Use area models to represent the distributive property in mathematical reasoning.
-
3 learning outcomes – click to view
Samples: Area using square tiles. Measure using square centimeters. Calculating area. Measure using square centimetres.
-
Area using a grid.
- Activities: 4 course, 11 extra
-
-
- Measure using square centimeters
- Tutorial
-
-
-
- Measure using square centimetres
- Tutorial
-
-
-
- Measure area using a grid tutorial
- Tutorial
-
Extra activities
-
-
- Drawing shapes that have a given area.
- Printable
-
-
-

- Compare area tutorial
- Tutorial
-
-
-

- Measuring area using informal units
- Practice
-
-
-

- Compare area
- Practice
-
-
-

- Measure area using a grid
- Practice
-
-
-

- Calculating area using a grid
- Practice
-
-
Square centimetres
- Activities: 1 course, 7 extra
-
-
- Calculating area
- Tutorial
-
Extra activities
-
-

- Area Problem Solving
- Assessment
-
-
-
- Area Problem Solving
- Printable
-
-
-

- Area Problem Solving
- Assessment
-
-
-
- Area Problem Solving
- Printable
-
-
-
- Area Problem Solving
- Printable
-
-
-
- Area
- Printable
-
-
-
- Area Problem Solving
- Printable
-
-
3 learning outcomes – click to view
3.MD.7.d – Recognize area as additive. Find areas of rectilinear figures by decomposing them into non-overlapping rectangles and adding the areas of the non-overlapping parts, applying this technique to solve real world problems.
-
2 learning outcomes – click to view
Samples: Calculating the Area of Irregular Shapes. Calculating the Area of Irregular Shapes. Area of irregular shapes.
-
Area of irregular shapes
- Activities: 3 course, 2 extra
-
-
- Area of irregular shapes
- Practice
-
-
-
- Area of irregular shapes
- Practice
-
Extra activities
-
-
- Area of irregular shapes
- Practice
-
-
-
- Calculating the Area of Irregular Shapes
- Printable
-
-
-
2 learning outcomes – click to view
Mathematics
3.MD.8 – Solve real world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters.
-
3 learning outcomes – click to view
Samples: Perimeter. Perimeter of irregular shapes. Perimeter and Area. Perimeter of squares and rectangles.
-
Perimeter of squares and rectangles.
- Activities: 3 course, 5 extra
-
-
- Perimeter
- Tutorial
-
-
-
- Perimeter of squares and rectangles
- Practice
-
-
-
- Calculating Perimeter Regular Shapes
- Tutorial
-
Extra activities
-
-
- Calculating perimeter tutorial
- Tutorial
-
-
-

- Perimeter problems
- Practice
-
-
-

- Measure Perimeter Using the Centimetre
- Whiteboard
-
-
-

- Calculating Perimeter
- Practice
-
-
Perimeter of irregular shapes.
- Activities: 3 course, 12 extra
-
-
- Perimeter of irregular shapes
- Practice
-
-
-
- Draw shapes - perimeter
- Printable
-
Extra activities
-
-
- Perimeter Problem Solving
- Printable
-
-
-
- Measuring perimeter in inches
- Printable
-
-
-
- Perimeter using centimeters and inches
- Printable
-
-
-
- Perimeter Problem Solving
- Printable
-
-
-

- Calculating Perimeter using Meters
- Practice
-
-
-

- Measuring perimeter in yards
- Practice
-
-
-

- Perimeter Problem Solving
- Assessment
-
-
-

- Perimeter Problem Solving
- Assessment
-
-
-
3 learning outcomes – click to view
3.G – Geometry
Mathematics
3.G.1 – Understand that shapes in different categories (e.g., rhombuses, rectangles, and others) may share attributes (e.g., having four sides), and that the shared attributes can define a larger category (e.g., quadrilaterals). Recognize rhombuses, rectangles, and squares as examples of quadrilaterals, and draw examples of quadrilaterals that do not belong to any of these subcategories.
-
4 learning outcomes – click to view
Samples: Tessellating patterns. Identifying types of lines. Shapes. Constructing 2D shapes. Tessellating patterns.
-
Identifying shapes based on attributes
- Activities: 4 course, 0 extra
-
-
- Tessellating patterns
- Tutorial
-
-
-
- Tessellating patterns
- Tutorial
-
-
-
- Identifying attributes of shapes
- Practice
-
-
Identifying types of lines
- Activities: 2 course, 2 extra
-
-
- Identifying types of lines
- Tutorial
-
-
-
- Identifying lines
- Practice
-
Extra activities
-
-
- Classifying lines
- Printable
-
-
-

- Identifying types of lines
- Practice
-
-
Construct and draw two dimensional shapes
- Activities: 3 course, 3 extra
-
-
- Constructing 2D shapes
- Tutorial
-
-
-
- Constructing 2D shapes
- Tutorial
-
-
-
- Drawing shapes
- Printable
-
Extra activities
-
-
- Drawing 2D shapes
- Printable
-
-
-

- Constructing 2D shapes
- Practice
-
-
-

- Draw Shapes
- Printable
-
-
-
4 learning outcomes – click to view
3.G.2 – Partition shapes into parts with equal areas. Express the area of each part as a unit fraction of the whole. For example, partition a shape into 4 parts with equal area, and describe the area of each part as 1/4 of the area of the shape.
-
6 learning outcomes – click to view
Samples: Fractions of an area. Equivalent Fractions. Comparing fractions as quantities. Hundredths in their lowest forms.
-
Fractions of an area
- Activities: 2 course, 1 extra
-
-
- Fractions of an area
- Practice
-
-
-
- Fractions of an area
- Practice
-
Extra activities
-
-
- Fractions - Area
- Printable
-
-
Comparing fractions as quantities.
- Activities: 1 course, 0 extra
-
-
- Comparing fractions as quantities
- Practice
-
-
Hundredths in their lowest forms
- Activities: 1 course, 0 extra
-
-
- Hundredths in their lowest forms
- Practice
-
-
Halves, quarters and eighths
- Activities: 7 course, 10 extra
-
-
- Quarters
- Tutorial
-
-
-
- Eighths
- Tutorial
-
-
-
- Halves and Quarters
- Practice
-
-
-
- Halves and quarters
- Tutorial
-
-
-
- Identifying Fractions
- Tutorial
-
Extra activities
-
-
- Quarters and eighths
- Printable
-
-
-
- Identifying fractions tutorial
- Tutorial
-
-
-
- Halves and quarters tutorial
- Tutorial
-
-
-
- Fraction of objects and shapes
- Practice
-
-
-

- Compare to a half tutorial
- Tutorial
-
-
-

- Compare to a half
- Practice
-
-
-

- Comparing fractions tutorial
- Tutorial
-
-
-
- Identifying halves and quarters
- Practice
-
-
-

- Comparing fractions
- Practice
-
-
-
6 learning outcomes – click to view