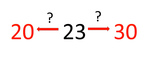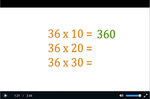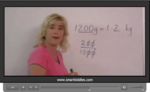Mathematics – United States – Common Core State Standards
4.OA – Operations & Algebraic Thinking
Mathematics
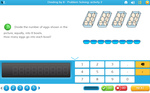
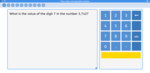
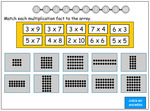
4.OA.1 – Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 × 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations.
-
1 learning outcomes – click to view
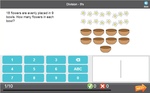
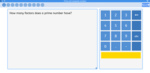
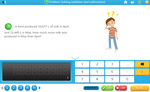
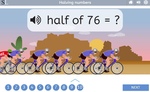
Samples: Multiplicative comparison. Multiplicative comparison (problem solving).
-
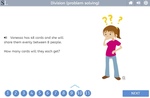
Multiplicative comparisons
- Activities: 2 course, 1 extra
-
-
1 learning outcomes – click to view
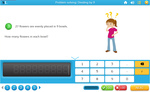
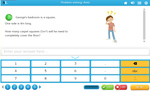
4.OA.2 – Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison. (See Glossary, Table 2. http://www.corestandards.org/the-standards/mathematics/glossary/glossary/ )
4.OA.3 – Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.
-
11 learning outcomes – click to view
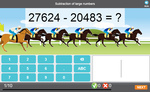
Samples: Two step problem solving. Make 100 Answer sheet. Challenge puzzle. Addition of large numbers (puzzle).
-
Two step problem solving
- Activities: 1 course, 0 extra
-
Make 100 - problem solving
- Activities: 0 course, 2 extra
-
Challenge puzzle - make 100
- Activities: 1 course, 0 extra
-
Addition of large numbers (puzzle)
- Activities: 1 course, 0 extra
-
Addition and subtraction - problem solving
- Activities: 1 course, 0 extra
-
Adding three two-digit numbers (problem solving)
- Activities: 2 course, 4 extra
-
Challenge puzzle - two digit subtraction
- Activities: 1 course, 0 extra
-
Subtracting from 1000 and 10000 (problem solving)
- Activities: 3 course, 2 extra
-
Dividing by 8 (problem solving)
- Activities: 3 course, 3 extra
-
Dividing by 9 (problem solving)
- Activities: 3 course, 6 extra
-
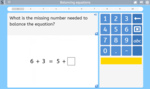
Balancing equations
- Activities: 2 course, 0 extra
-
-
11 learning outcomes – click to view
Mathematics
4.OA.4 – Find all factor pairs for a whole number in the range 1–100. Recognize that a whole number is a multiple of each of its factors. Determine whether a given whole number in the range 1–100 is a multiple of a given one-digit number. Determine whether a given whole number in the range 1–100 is prime or composite.
-
8 learning outcomes – click to view
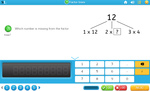
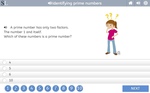
Samples: Factor trees. Factors. Common factors. Prime and Composite Numbers. Factors. Prime numbers.
-
Factor trees
- Activities: 1 course, 0 extra
-
Identifying factors
- Activities: 3 course, 2 extra
-
Common factors
- Activities: 2 course, 0 extra
-
Prime and Composite Numbers
- Activities: 1 course, 0 extra
-
Factors
- Activities: 7 course, 3 extra
-
Prime and composite numbers
- Activities: 3 course, 1 extra
-
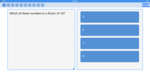
Identifying prime numbers < 100 (puzzle)
- Activities: 1 course, 0 extra
-
Identifying prime numbers
- Activities: 1 course, 0 extra
-
-
8 learning outcomes – click to view
Mathematics
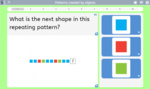
4.OA.5 – Generate a number or shape pattern that follows a given rule. Identify apparent features of the pattern that were not explicit in the rule itself. For example, given the rule “Add 3” and the starting number 1, generate terms in the resulting sequence and observe that the terms appear to alternate between odd and even numbers. Explain informally why the numbers will continue to alternate in this way.
-
4 learning outcomes – click to view
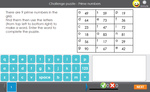
Samples: Patterns created by objects. Number Patterns (2,3,5,10). Number patterns - Identifying the rule.
-
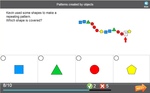
Explore patterns created by objects
- Activities: 2 course, 0 extra
-
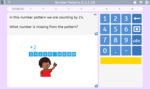
Number Patterns (2,3,5,10)
- Activities: 2 course, 5 extra
-
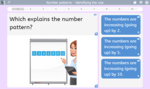
Number patterns - Identifying the rule
- Activities: 2 course, 0 extra
-
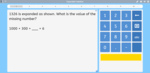
Continue number patterns resulting from addition or subtraction
- Activities: 1 course, 1 extra
-
-
4 learning outcomes – click to view
4.NBT – Number & Operations in Base Ten (Grade 4 expectations in this domain are limited to whole numbers less than or equal to 1,000,000.)
Mathematics
4.NBT.1 – Recognize that in a multi-digit whole number, a digit in one place represents ten times what it represents in the place to its right. For example, recognize that 700 ÷ 70 = 10 by applying concepts of place value and division.
4.NBT.2 – Read and write multi-digit whole numbers using base-ten numerals, number names, and expanded form. Compare two multi-digit numbers based on meanings of the digits in each place, using >, =, and < symbols to record the results of comparisons.
-
26 learning outcomes – click to view
Samples: Expanded notation (to 10,000). Comparing numbers to 1000 (< = >). Write numbers – to 1000.
-
Expanded notation (to 10,000)
- Activities: 4 course, 5 extra
-
Comparing numbers to 1000 (< = >)
- Activities: 2 course, 1 extra
-
Writing numbers – to 1000
- Activities: 2 course, 2 extra
-
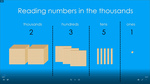
Reading numbers – to 1000
- Activities: 1 course, 0 extra
-
Comparing numbers – to 1000
- Activities: 1 course, 1 extra
-
Reading numbers to 10,000
- Activities: 1 course, 0 extra
-
Writing numbers to 10,000
- Activities: 2 course, 0 extra
-
Comparing numbers – to 10,000
- Activities: 1 course, 0 extra
-
Place value - thousands, hundreds, tens and ones
- Activities: 7 course, 12 extra
-
Comparing numbers to 10,000 (<,=,>)
- Activities: 1 course, 0 extra
-
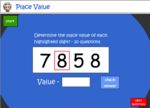
Place value of a digit
- Activities: 3 course, 1 extra
-
Odd and even numbers
- Activities: 3 course, 2 extra
-
Challenge puzzle - Odd and Even Numbers
- Activities: 1 course, 0 extra
-
Write numbers – to 100,000
- Activities: 2 course, 0 extra
-
Reading numbers – to 100,000
- Activities: 1 course, 0 extra
-
Comparing numbers – to 100,000
- Activities: 1 course, 0 extra
-
Reading large numbers
- Activities: 1 course, 0 extra
-
Ordering large numbers
- Activities: 0 course, 6 extra
-
Write numbers – to 1,000,000
- Activities: 2 course, 0 extra
-
Comparing large numbers
- Activities: 2 course, 0 extra
-
Large numbers presented in tables
- Activities: 1 course, 0 extra
-
Reading large numbers
- Activities: 1 course, 0 extra
-
Write numbers – over one million
- Activities: 2 course, 0 extra
-
Comparing numbers of any size
- Activities: 1 course, 0 extra
-
Challenge puzzle - flow diagram
- Activities: 1 course, 0 extra
-
-
26 learning outcomes – click to view
4.NBT.3 – Use place value understanding to round multi-digit whole numbers to any place.
-
2 learning outcomes – click to view
Samples: Rounding to the nearest 10 (3 digits). Rounding to the nearest hundred. Rounding numbers: Activity 2.
-
Rounding to the nearest 10
- Activities: 3 course, 3 extra
-
Rounding to the nearest hundred
- Activities: 3 course, 0 extra
-
-
2 learning outcomes – click to view
Mathematics
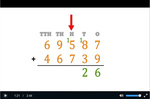
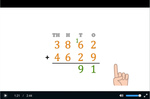
4.NBT.4 – Fluently add and subtract multi-digit whole numbers using the standard algorithm.
-
9 learning outcomes – click to view
Samples: Subtracting three digit numbers. Subtracting from multiples of one thousand.
-
Subtracting three digit numbers
- Activities: 2 course, 0 extra
-
Subtracting from 1000
- Activities: 6 course, 10 extra
-
Adding three two-digit numbers (mental strategy)
- Activities: 6 course, 10 extra
-
Subtracting large numbers
- Activities: 3 course, 14 extra
-
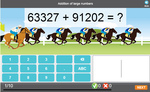
Adding large numbers
- Activities: 5 course, 29 extra
-
Addition and subtraction (problem solving)
- Activities: 3 course, 4 extra
-
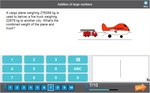
Adding large numbers (problem solving)
- Activities: 1 course, 8 extra
-
Subtracting from 1000 (problem solving)
- Activities: 1 course, 4 extra
-
Subtracting large numbers
- Activities: 4 course, 6 extra
-
-
9 learning outcomes – click to view
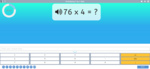
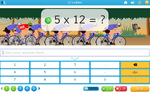
4.NBT.5 – Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
-
13 learning outcomes – click to view
Samples: Adding on to Multiples of 10. Multiplying 2 by 1 digit (mental strategy).
-
Adding-on to multiples of ten
- Activities: 2 course, 1 extra
-
Multiplying a two-digit number by a one-digit number
- Activities: 1 course, 2 extra
-
Multiplying a two-digit number by a one-digit number (written strategy)
- Activities: 4 course, 13 extra
-
Multiplying a two-digit number by a one-digit number - mental strategy
- Activities: 4 course, 10 extra
-
Multiplying 2 digits by a 1 digit number - Puzzle
- Activities: 1 course, 0 extra
-
Multiplying multiples of 10 (missing number)
- Activities: 3 course, 8 extra
-
Multiplying by multiples of ten
- Activities: 4 course, 12 extra
-
Multiples of 10 by 1 digit - problem solving
- Activities: 0 course, 1 extra
-
Arrays
- Activities: 0 course, 1 extra
-
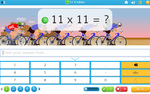
11x tables
- Activities: 2 course, 1 extra
-
12x tables
- Activities: 2 course, 1 extra
-
Multiplying multiples of 10 (problem solving)
- Activities: 2 course, 1 extra
-
Multiples
- Activities: 2 course, 1 extra
-
-
13 learning outcomes – click to view
4.NBT.6 – Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
-
10 learning outcomes – click to view
Samples: Dividing two-digits by one-digit. Dividing multiples of 10 by 1 digit.
-
Dividing two-digits by one-digit (no remainders)
- Activities: 7 course, 9 extra
-
Dividing multiples of ten by one-digit
- Activities: 4 course, 2 extra
-
Dividing three-digits by one-digit
- Activities: 3 course, 7 extra
-
Division (with remainders)
- Activities: 3 course, 7 extra
-
Dividing whole numbers by 100
- Activities: 4 course, 0 extra
-
Dividing a four-digit numbers by a one-digit number
- Activities: 4 course, 5 extra
-
Dividing multiples of 10 by 1 digit (problem solving)
- Activities: 0 course, 1 extra
-
Dividing 3 digits by 1 digit (problem solving)
- Activities: 0 course, 2 extra
-
Halving numbers
- Activities: 4 course, 5 extra
-
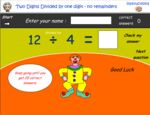
Division (problem solving)
- Activities: 2 course, 7 extra
-
-
10 learning outcomes – click to view
4.NF – Number & Operations—Fractions (Grade 4 expectations in this domain are limited to fractions with denominators 2, 3, 4, 5, 6, 8, 10, 12, 100.)
Mathematics
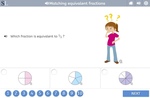
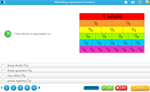
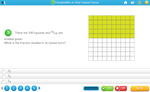
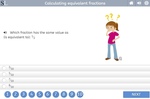
4.NF.1 – Explain why a fraction a/b is equivalent to a fraction (n × a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions.
-
4 learning outcomes – click to view
Samples: Modelling equivalent fractions. Hundredths in their lowest forms. Equivalent fractions.
-
Modelling equivalent fractions
- Activities: 4 course, 3 extra
-
Hundredths in their lowest forms
- Activities: 1 course, 0 extra
-
Equivalent fractions
- Activities: 9 course, 11 extra
-
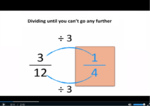
Simplifying fractions
- Activities: 4 course, 2 extra
-
-
4 learning outcomes – click to view
4.NF.2 – Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
-
3 learning outcomes – click to view
Samples: Comparing fractions to a half. Hundredths - simplest form. Comparing Fractions.
-
Comparing fractions
- Activities: 4 course, 0 extra
-
Tenths and hundredths
- Activities: 4 course, 4 extra
-
Comparing fractions
- Activities: 4 course, 2 extra
-
-
3 learning outcomes – click to view
Mathematics
4.NF.3 – Understand a fraction a/b with a > 1 as a sum of fractions 1/b.
4.NF.3.a – Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
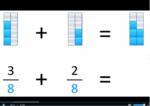
4.NF.3.b – Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8 ; 3/8 = 1/8 + 2/8 ; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8.
-
3 learning outcomes – click to view
Samples: Adding fractions - same denominators. Adding fraction with common denominators tutorial.
-
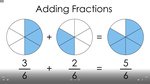
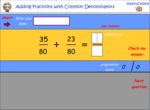
Adding and subtracting fractions - common denominators
- Activities: 5 course, 1 extra
-
Add and subtract fractions (same denominators)
- Activities: 0 course, 3 extra
-
Adding and subtracting related fractions
- Activities: 6 course, 3 extra
-
-
3 learning outcomes – click to view
4.NF.3.c – Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
-
4 learning outcomes – click to view
Samples: Adding fraction with common denominators tutorial. Converting Improper Fractions.
-
Add and subtract fractions (same denominators)
- Activities: 0 course, 3 extra
-
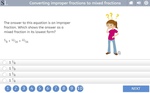
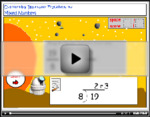
Improper and mixed number fractions
- Activities: 6 course, 1 extra
-
Converting mixed numbers to improper frac.
- Activities: 0 course, 1 extra
-
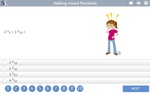
Adding mixed fractions
- Activities: 1 course, 0 extra
-
-
4 learning outcomes – click to view
4.NF.3.d – Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.
-
2 learning outcomes – click to view
Samples: Adding fraction with common denominators tutorial. Adding and subtracting related fractions.
-
Add and subtract fractions (same denominators)
- Activities: 0 course, 3 extra
-
Adding and subtracting related fractions
- Activities: 6 course, 3 extra
-
-
2 learning outcomes – click to view
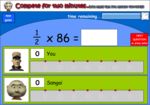
4.NF.4 – Apply and extend previous understandings of multiplication to multiply a fraction by a whole number.
4.NF.4.a – Understand a fraction a/b as a multiple of 1/b. For example, use a visual fraction model to represent 5/4 as the product 5 × (1/4), recording the conclusion by the equation 5/4 = 5 × (1/4).
-
2 learning outcomes – click to view
Samples: Fractions. Fractions of a number. Fractions of a number. Fractions of a number.
-
Multiplying fractions by a whole number - visual
- Activities: 1 course, 0 extra
-
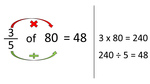
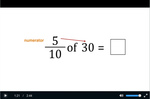
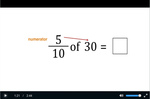
Fractions of a number
- Activities: 9 course, 4 extra
-
-
2 learning outcomes – click to view
4.NF.4.b – Understand a multiple of a/b as a multiple of 1/b, and use this understanding to multiply a fraction by a whole number. For example, use a visual fraction model to express 3 × (2/5) as 6 × (1/5), recognizing this product as 6/5. (In general, n × (a/b) = (n × a)/b.)
-
2 learning outcomes – click to view
Samples: Fractions. Fractions of a number. Fractions of a number. Fractions of a number.
-
Multiplying fractions by a whole number - visual
- Activities: 1 course, 0 extra
-
Fractions of a number
- Activities: 9 course, 4 extra
-
-
2 learning outcomes – click to view
4.NF.4.c – Solve word problems involving multiplication of a fraction by a whole number, e.g., by using visual fraction models and equations to represent the problem. For example, if each person at a party will eat 3/8 of a pound of roast beef, and there will be 5 people at the party, how many pounds of roast beef will be needed? Between what two whole numbers does your answer lie?
-
1 learning outcomes – click to view
Samples: Fractions of quantities (problem solving). Fractions Problem Solving.
-
Simple fractions of quantities (problem solving)
- Activities: 1 course, 1 extra
-
-
1 learning outcomes – click to view
Mathematics
4.NF.5 – Express a fraction with denominator 10 as an equivalent fraction with denominator 100, and use this technique to add two fractions with respective denominators 10 and 100. (Students who can generate equivalent fractions can develop strategies for adding fractions with unlike denominators in general. But addition and subtraction with unlike denominators in general is not a requirement at this grade.) For example, express 3/10 as 30/100, and add 3/10 + 4/100 = 34/100.
-
1 learning outcomes – click to view
Samples: Hundredths - simplest form. Tenths and hundredths. Tenths and hundreds (problem solving).
-
Tenths and hundredths
- Activities: 4 course, 4 extra
-
-
1 learning outcomes – click to view
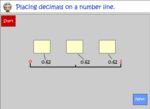
4.NF.6 – Use decimal notation for fractions with denominators 10 or 100. For example, rewrite 0.62 as 62/100; describe a length as 0.62 meters; locate 0.62 on a number line diagram.
-
3 learning outcomes – click to view
Samples: Converting 10ths and 100ths to decimals. Placing Decimals On A Number Line. Comparing fractions and decimals.
-
Converting 10ths and 100ths to decimals
- Activities: 1 course, 0 extra
-
Decimals on a number line.
- Activities: 2 course, 2 extra
-
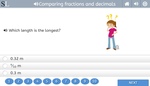
Comparing fractions and decimals (10ths 100ths)
- Activities: 1 course, 0 extra
-
-
3 learning outcomes – click to view
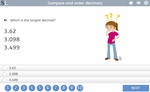
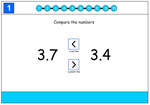
4.NF.7 – Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual model.
-
4 learning outcomes – click to view
Samples: Compare and order decimals. Comparing Fractions. Comparing fractions to a half. Equivalent fractions.
-
Compare and order decimals
- Activities: 1 course, 1 extra
-
Comparing fractions
- Activities: 4 course, 2 extra
-
Comparing fractions
- Activities: 4 course, 0 extra
-
Equivalent fractions
- Activities: 9 course, 11 extra
-
-
4 learning outcomes – click to view
4.MD – Measurement & Data
Mathematics
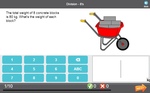
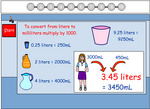
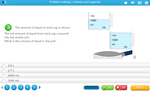
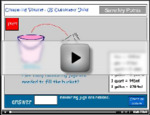
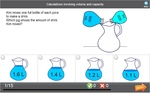
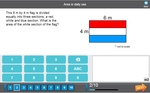
4.MD.1 – Know relative sizes of measurement units within one system of units including km, m, cm; kg, g; lb, oz.; l, ml; hr, min, sec. Within a single system of measurement, express measurements in a larger unit in terms of a smaller unit. Record measurement equivalents in a two-column table. For example, know that 1 ft is 12 times as long as 1 in. Express the length of a 4 ft snake as 48 in. Generate a conversion table for feet and inches listing the number pairs (1, 12), (2, 24), (3, 36), ...
-
9 learning outcomes – click to view
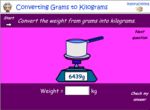
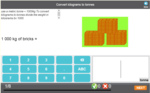
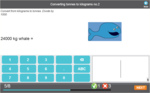
Samples: Converting between grams and kilograms. Common fractions of a kilogram. Convert Tonnes To Kilograms.
-
Converting between grams and kilograms
- Activities: 1 course, 0 extra
-
Convert units of mass - between kilograms and grams
- Activities: 6 course, 22 extra
-
Convert units of mass - between kilograms and tonnes
- Activities: 2 course, 11 extra
-
Convert between units of mass
- Activities: 1 course, 0 extra
-
Converting between kilometers and meters
- Activities: 2 course, 0 extra
-
Converting between metric units of length.
- Activities: 1 course, 8 extra
-
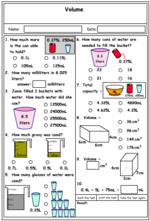
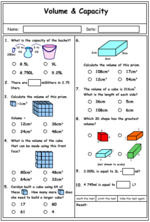
Problem solving : Volume
- Activities: 0 course, 5 extra
-
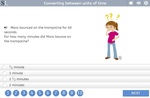
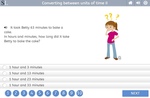
Converting between units of time
- Activities: 2 course, 0 extra
-
Convert between units of time
- Activities: 2 course, 1 extra
-
-
9 learning outcomes – click to view
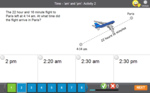
4.MD.2 – Use the four operations to solve word problems involving distances, intervals of time, liquid volumes, masses of objects, and money, including problems involving simple fractions or decimals, and problems that require expressing measurements given in a larger unit in terms of a smaller unit. Represent measurement quantities using diagrams such as number line diagrams that feature a measurement scale.
-
3 learning outcomes – click to view
Samples: Volume and Capacity. Calculating cost according to weight - US units tutorial. Time - 'am' and 'pm': Activity 1.
-
Volume and Capacity
- Activities: 2 course, 7 extra
-
Mass (problem solving)
- Activities: 0 course, 2 extra
-
Use a.m. and p.m.
- Activities: 0 course, 2 extra
-
-
3 learning outcomes – click to view
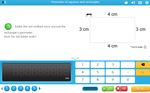
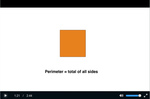
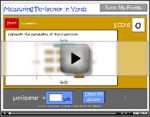
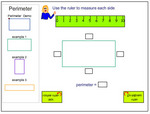
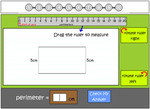
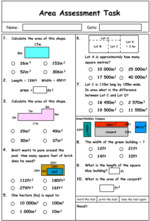
4.MD.3 – Apply the area and perimeter formulas for rectangles in real world and mathematical problems. For example, find the width of a rectangular room given the area of the flooring and the length, by viewing the area formula as a multiplication equation with an unknown factor.
-
4 learning outcomes – click to view
Samples: Perimeter. Challenge puzzle -perimeter. Area. Area (problem solving). Perimeter of squares and rectangles.
-
Perimeter of squares and rectangles.
- Activities: 3 course, 5 extra
-
Challenge puzzle -perimeter
- Activities: 1 course, 0 extra
-
Area
- Activities: 1 course, 0 extra
-
Area (problem solving)
- Activities: 2 course, 7 extra
-
-
4 learning outcomes – click to view
Mathematics
4.MD.4 – Make a line plot to display a data set of measurements in fractions of a unit (1/2, 1/4, 1/8). Solve problems involving addition and subtraction of fractions by using information presented in line plots. For example, from a line plot find and interpret the difference in length between the longest and shortest specimens in an insect collection.
Mathematics
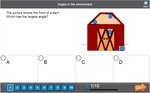
4.MD.5 – Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement:
4.MD.5.a – An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of the circular arc between the points where the two rays intersect the circle. An angle that turns through 1/360 of a circle is called a “one-degree angle,” and can be used to measure angles.
-
2 learning outcomes – click to view
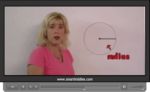
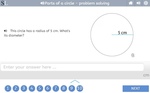
Samples: Angles within a circle. Parts of a circle. Parts of a circle. Learn the parts of a circle. Parts of a circle.
-
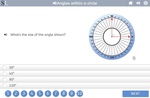
Angles within a circle
- Activities: 1 course, 0 extra
-
Parts of a Circle
- Activities: 5 course, 0 extra
-
-
2 learning outcomes – click to view
4.MD.5.b – An angle that turns through n one-degree angles is said to have an angle measure of n degrees.
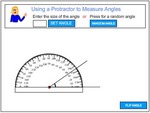
4.MD.6 – Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.
-
6 learning outcomes – click to view
Samples: Comparing angles. Right angles in shapes. Measuring obtuse angles using a protractor. Estimating the size of angles.
-
Comparing angles
- Activities: 2 course, 1 extra
-
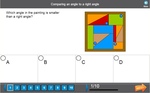
Comparing to a right angle
- Activities: 4 course, 3 extra
-
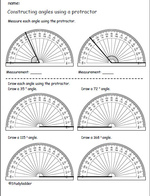
Measuring obtuse angles using a protractor
- Activities: 1 course, 3 extra
-
Estimate the size of angles.
- Activities: 1 course, 0 extra
-
Measure and classify angles.
- Activities: 1 course, 2 extra
-
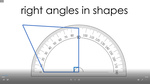
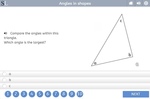
Angles in shapes
- Activities: 1 course, 0 extra
-
-
6 learning outcomes – click to view
4.MD.7 – Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems, e.g., by using an equation with a symbol for the unknown angle measure.
-
8 learning outcomes – click to view
Samples: Angles on a straight line. Measuring obtuse angles using a protractor. Estimating the size of angles.
-
Angles on a straight line
- Activities: 2 course, 1 extra
-
Measuring obtuse angles using a protractor
- Activities: 1 course, 3 extra
-
Estimate the size of angles.
- Activities: 1 course, 0 extra
-
Angles within a circle
- Activities: 1 course, 0 extra
-
Naming angles
- Activities: 5 course, 3 extra
-
Naming angles within shapes
- Activities: 1 course, 0 extra
-
Measure and classify angles.
- Activities: 1 course, 2 extra
-
Angles in shapes
- Activities: 1 course, 0 extra
-
-
8 learning outcomes – click to view
4.G – Geometry
Mathematics
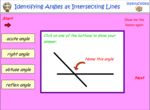
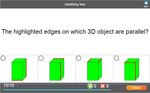
4.G.1 – Draw points, lines, line segments, rays, angles (right, acute, obtuse), and perpendicular and parallel lines. Identify these in two-dimensional figures.
-
3 learning outcomes – click to view
Samples: Identifying types of lines. Types of angles. Naming angles within shapes. Identifying lines.
-
Identifying types of lines
- Activities: 2 course, 2 extra
-
Naming angles
- Activities: 5 course, 3 extra
-
Naming angles within shapes
- Activities: 1 course, 0 extra
-
-
3 learning outcomes – click to view
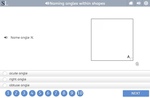
4.G.2 – Classify two-dimensional figures based on the presence or absence of parallel or perpendicular lines, or the presence or absence of angles of a specified size. Recognize right triangles as a category, and identify right triangles.
-
6 learning outcomes – click to view
Samples: Comparing angles. Right angles in shapes. Identifying types of lines. Properties of two-dimensional shapes.
-
Comparing angles
- Activities: 2 course, 1 extra
-
Comparing to a right angle
- Activities: 4 course, 3 extra
-
Identifying types of lines
- Activities: 2 course, 2 extra
-
Attributes of two dimensional shapes
- Activities: 2 course, 0 extra
-
Grouping shapes based on attributes
- Activities: 1 course, 0 extra
-
Naming triangles
- Activities: 4 course, 0 extra
-
-
6 learning outcomes – click to view
4.G.3 – Recognize a line of symmetry for a two-dimensional figure as a line across the figure such that the figure can be folded along the line into matching parts. Identify line-symmetric figures and draw lines of symmetry.
-
4 learning outcomes – click to view
Samples: Symmetry in the environment. Creating Symmetrical Drawings and Patterns. Identify line of symmetry.
-
Symmetry - man-made structures
- Activities: 0 course, 1 extra
-
Drawing symmetrical pictures
- Activities: 0 course, 4 extra
-
Lines of symmetry
- Activities: 1 course, 1 extra
-
Rotational symmetry
- Activities: 2 course, 1 extra
-
-
4 learning outcomes – click to view